Lời giải
Gọi x là số ha khu đất trồng ngô, nó là số ha khu đất trồng đỗ xanh.
Ta với những ĐK buộc ràng so với x, nó như sau:
⦁ Hiển nhiên x ≥ 0, nó ≥ 0.
⦁ Diện tích canh tác ko vượt lên vượt 8 ha nên tao với x + nó ≤ 8.
⦁ Số ngày công dùng ko vượt lên vượt 180 ngày nên 20x + 30y ≤ 180.
⇔ 2x + 3y ≤ 18.
Từ cơ, tao với hệ bất phương trình tế bào mô tả những ĐK buộc ràng là:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + nó \le 8\\2x + 3y \le 18\end{array} \right.\,\,\left( * \right)\).
Yêu cầu Việc ⇔ Tìm (x; y) thỏa (*) nhằm F(x; y) = 40x + 50y đạt độ quý hiếm lớn số 1.
Vẽ và xác lập miền nghiệm của (*):
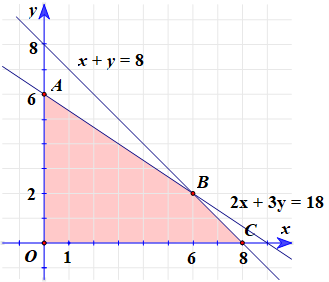
Ta có:
⦁ Miền nghiệm của (*) là tứ giác OABC (kể cả biên).
⦁ O(0; 0), A(0; 6), B(6; 2), C(8; 0).
⦁ F(O) = 0, F(A) = 300, F(B) = 340, F(C) = 320.
Suy rời khỏi maxF(x; y) = F(B) = 340 Lúc và chỉ Lúc x = 6, nó = 2.
Vậy nhằm thu được không ít chi phí nhất thì chưng Năm cần thiết trồng 6 ha ngô và 2 ha đỗ xanh.
Câu 2:
Trong lớp 10C với 16 học viên xuất sắc Toán, 15 học viên xuất sắc Lí, 11 học viên xuất sắc Hóa. tường rằng với 9 học viên một vừa hai phải xuất sắc Toán và Lí, 6 học viên một vừa hai phải xuất sắc Lí và Hóa, 8 học viên một vừa hai phải xuất sắc Hóa và Toán, nhập cơ với 11 học viên xuất sắc đích 2 môn. Hỏi với từng nào học viên nhập lớp:
a) Giỏi cả tía môn.
b) Giỏi đích 1 môn.
Trong lớp 10C với 16 học viên xuất sắc Toán, 15 học viên xuất sắc Lí, 11 học viên xuất sắc Hóa. tường rằng với 9 học viên một vừa hai phải xuất sắc Toán và Lí, 6 học viên một vừa hai phải xuất sắc Lí và Hóa, 8 học viên một vừa hai phải xuất sắc Hóa và Toán, nhập cơ với 11 học viên xuất sắc đích 2 môn. Hỏi với từng nào học viên nhập lớp:
a) Giỏi cả tía môn.
b) Giỏi đích 1 môn.
Câu 3:
Cho tứ diện đều ABCD, cạnh a. Gọi I, J theo lần lượt là trung điểm của AC, BC. Gọi K là một trong điểm bên trên cạnh BD sao mang lại KB = 2KD.
a) Xác toan tiết diện của tứ diện với mặt mày phẳng phiu (IJK). Chứng minh tiết diện là hình thang cân nặng.
b) Tính diện tích S tiết diện cơ.
Cho tứ diện đều ABCD, cạnh a. Gọi I, J theo lần lượt là trung điểm của AC, BC. Gọi K là một trong điểm bên trên cạnh BD sao mang lại KB = 2KD.
a) Xác toan tiết diện của tứ diện với mặt mày phẳng phiu (IJK). Chứng minh tiết diện là hình thang cân nặng.
b) Tính diện tích S tiết diện cơ.
Câu 4:
Cho tam giác ABC. Gọi I là vấn đề bên trên cạnh BC sao mang lại 2CI = 3BI và J là vấn đề bên trên BC kéo dãn dài sao mang lại 5JB = 2JC. Gọi G là trọng tâm tam giác.
a) Biểu thao diễn \(\overrightarrow {AB} ,\overrightarrow {AC} \) theo đòi nhị vectơ \(\overrightarrow {AI} ,\overrightarrow {AJ} \) và màn biểu diễn \(\overrightarrow {AJ} \) qua quýt \(\overrightarrow {AB} ,\overrightarrow {AC} \).
b) Biểu thao diễn \(\overrightarrow {AG} \) theo đòi nhị vectơ \(\overrightarrow {AI} ,\overrightarrow {AJ} \).
Cho tam giác ABC. Gọi I là vấn đề bên trên cạnh BC sao mang lại 2CI = 3BI và J là vấn đề bên trên BC kéo dãn dài sao mang lại 5JB = 2JC. Gọi G là trọng tâm tam giác.
a) Biểu thao diễn \(\overrightarrow {AB} ,\overrightarrow {AC} \) theo đòi nhị vectơ \(\overrightarrow {AI} ,\overrightarrow {AJ} \) và màn biểu diễn \(\overrightarrow {AJ} \) qua quýt \(\overrightarrow {AB} ,\overrightarrow {AC} \).
b) Biểu thao diễn \(\overrightarrow {AG} \) theo đòi nhị vectơ \(\overrightarrow {AI} ,\overrightarrow {AJ} \).
Câu 5:
Cho tam giác ABC, lấy những điểm M, N, Phường sao mang lại \(\overrightarrow {MB} = 3\overrightarrow {MC} \); \(\overrightarrow {NA} + 3\overrightarrow {NC} = \vec 0\) và \(\overrightarrow {PA} + \overrightarrow {PB} = \vec 0\).
a) Tính \(\overrightarrow {PM} ,\,\,\overrightarrow {PN} \) theo đòi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b) Chứng minh rằng: M, N, Phường trực tiếp sản phẩm.
Cho tam giác ABC, lấy những điểm M, N, Phường sao mang lại \(\overrightarrow {MB} = 3\overrightarrow {MC} \); \(\overrightarrow {NA} + 3\overrightarrow {NC} = \vec 0\) và \(\overrightarrow {PA} + \overrightarrow {PB} = \vec 0\).
a) Tính \(\overrightarrow {PM} ,\,\,\overrightarrow {PN} \) theo đòi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b) Chứng minh rằng: M, N, Phường trực tiếp sản phẩm.
