Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. a) Chứng minh rằng (AFD) // (BEC). b) Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song (Miễn phí)

Lời giải

a)

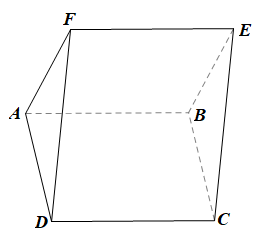
Ta có: BE // AF (do ABEF là hình bình hành);

            AF ⊂ (AFD)

Do bại BE // (AFD).

Ta cũng có: BC // AD (do ABCD là hình bình hành)

                    AD ⊂ (AFD)

Do bại BC // (AFD).

Do BE // (AFD);

      BC // (AFD);

      BE, BC rời nhau bên trên điểm B và nằm trong lệ thuộc mp(BEC)

Suy đi ra (AFD) // (BEC).

b)

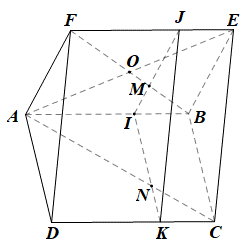
+) Do (AFD) tuy vậy song với (P) nên tồn bên trên hai tuyến phố trực tiếp nhập (AFD) tuy vậy song với (P).

• Trong mp(ABEF), qua chuyện điểm M vẽ đường thẳng liền mạch tuy vậy song với AF, đường thẳng liền mạch này rời AB, EF theo lần lượt bên trên I, J.

Khi bại IJ // AF, tuy nhiên AF ⊂ (AFD) nên IJ // (AFD).

• Trong mp(ABCD), qua chuyện điểm I vẽ đường thẳng liền mạch tuy vậy song với AD, rời CD bên trên K.

Khi bại IK // AD, tuy nhiên AD ⊂ (AFD) nên IK // (AFD).

• Ta có: IJ // (AFD);

             IK // (AFD);

             IJ, IK rời nhau bên trên điểm I và nằm trong lệ thuộc mp(IJK).

Do bại (IJK) // (AFD).

Mà M ∈ IJ, IJ ⊂ (IJK) nên mp (P) trải qua M và tuy vậy song với (AFD) đó là mp(IJK).

+) Trong mp(ABCD), AC rời IK bên trên N, Khi bại N là gửi gắm điểm của AC và (P).

Trong mp(ABCD), xét DABC sở hữu IN // BC (do IK // AD // BC) nên bám theo lăm le lí Thalès tớ có: \[\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}}\].

Trong mp(ABEF), xét DABF sở hữu IM // AF nên bám theo lăm le lí Thalès tớ có: \[\frac{{AI}}{{IB}} = \frac{{FM}}{{MB}}\].

Gọi O là tâm hình bình hành ABEF. Khi bại O là trung điểm của FB nên FO = OB.

Do M là trọng tâm của DABE nên \(MB = \frac{2}{3}OB\) và \(OM = \frac{1}{3}OB\).

Ta có: \[\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}} = \frac{{FM}}{{MB}} = \frac{{FO + OM}}{{MB}} = \frac{{OB + \frac{1}{3}OB}}{{\frac{2}{3}OB}} = \frac{{\frac{4}{3}OB}}{{\frac{2}{3}OB}} = 2\].

Vậy \(\frac{{AM}}{{NC}} = 2\).

Câu 1:

Câu 5: