Câu hỏi:
12/07/2024 212,294
Cho hình chóp S.ABCD đem lòng ABCD là hình bình hành tâm O. Gọi M, N, Phường theo lần lượt là trung điểm của những đoạn BC, CD, SO. Tìm kí thác tuyến của (MNP) với những mặt mày bằng (SAB), (SAD), (SBC) và (SCD).
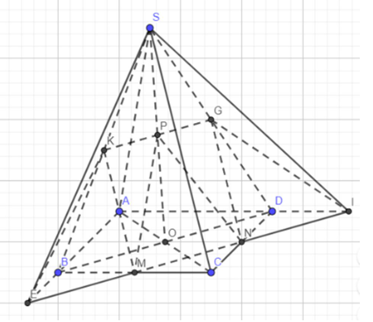
Gọi I, E theo lần lượt là kí thác điểm của MN với AD, AB
Qua Phường kẻ đường thẳng liền mạch tuy nhiên song với BD tách SB, SD theo lần lượt bên trên K, G
Ta có:
M, N theo lần lượt là trung điểm của BC, CD ⇒ MN là đàng khoảng của ∆BCD ⇒ MN // BD
Mà KG // BD ⇒ MN // KG ⇒ K, G ∈ (MNP)
Ta có:
+) \(\left\{ {\begin{array}{*{20}{c}}{E = AB \cap MN \Rightarrow E \in \left( {SAB} \right) \cap \left( {MNP} \right)}\\{K \in SB;K \in \left( {MNP} \right) \Rightarrow K \in \left( {SAB} \right) \cap \left( {MNP} \right)}\end{array}} \right. \Rightarrow \left( {SAB} \right) \cap \left( {MNP} \right) = KE\)
+) \(\left\{ {\begin{array}{*{20}{c}}{I = AD \cap MN \Rightarrow I \in \left( {SAD} \right) \cap \left( {MNP} \right)}\\{G \in SD;G \in \left( {MNP} \right) \Rightarrow G \in \left( {SAD} \right) \cap \left( {MNP} \right)}\end{array}} \right. \Rightarrow \left( {SAD} \right) \cap \left( {MNP} \right) = IG\)
+) \(\left\{ {\begin{array}{*{20}{c}}{M,K \in \left( {MNP} \right)}\\{M,K \in \left( {SBC} \right)}\end{array}} \right. \Rightarrow \left( {SBC} \right) \cap \left( {MNP} \right) = MK\)
+) \(\left\{ {\begin{array}{*{20}{c}}{N,G \in \left( {MNP} \right)}\\{N,G \in \left( {SCD} \right)}\end{array}} \right. \Rightarrow \left( {SCD} \right) \cap \left( {MNP} \right) = NG\)
Vậy (SAB) ∩ (MNP) = KE; (SAD) ∩ (MNP) = IG; (SBC) ∩ (MNP) = MK; (SCD) ∩ (MNP) = NG.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tính tổng: \({\sin ^2}2^\circ + {\sin ^2}4^\circ + {\sin ^2}6^\circ + ... + {\sin ^2}84^\circ + {\sin ^2}86^\circ + {\sin ^2}88^\circ \).
Câu 2:
Giá trị của
\(M = {\cos ^2}15 + {\cos ^2}25 + {\cos ^2}35 + {\cos ^2}45 + {\cos ^2}105 + {\cos ^2}115 + {\cos ^2}125\)là ?
Giá trị của
\(M = {\cos ^2}15 + {\cos ^2}25 + {\cos ^2}35 + {\cos ^2}45 + {\cos ^2}105 + {\cos ^2}115 + {\cos ^2}125\)là ?
Câu 3:
Cho hình thang ABCD (AB // CD) đem AD = CD và AC ⊥ BC. Từ C kẻ đường thẳng liền mạch tuy nhiên song với AD và tách AB bên trên E.
a. Chứng minh tứ giác AECD là hình thoi.
b. Chứng minh tứ giác BEDC là hình bình hành.
c. Chứng minh ∆CEB cân nặng.
Cho hình thang ABCD (AB // CD) đem AD = CD và AC ⊥ BC. Từ C kẻ đường thẳng liền mạch tuy nhiên song với AD và tách AB bên trên E.
a. Chứng minh tứ giác AECD là hình thoi.
b. Chứng minh tứ giác BEDC là hình bình hành.
c. Chứng minh ∆CEB cân nặng.
Câu 4:
Cho hình chóp S.ABCD đem lòng ABCD là hình thoi tâm O, cạnh A, \(\widehat {BAD} = 120^\circ \). Hai mặt mày bằng (SAB) và (SCD) nằm trong vuông góc với mặt mày lòng, (SC;(ABCD)) = 45°. Gọi G là trọng tâm ∆ABC, tính khoảng cách h kể từ G cho tới (SCD) theo gót a.
Câu 5:
Tìm GTNN của biểu thức \(A = \frac{{x + 7}}{{\sqrt x + 3}}\).
Câu 6:
Một tòa mái ấm đem n tầng, những tần được viết số từ là một cho tới n theo gót trật tự kể từ bên dưới lên bên trên. Có 4 cầu thang máy đang được tại tầng 1. tường rằng từng cầu thang máy rất có thể giới hạn ở đích thị 3 tầng (không kể tầng 1) và 3 tầng này sẽ không là 3 tầng số nguyên vẹn tiếp tục với 2 tầng bất kì (khác tầng 1) của tòa mái ấm luôn luôn có một cầu thang máy giới hạn được ở cả hai tầng này. Hỏi GTLN của n là bao nhiêu?
