Câu hỏi:
27/02/2024 41,401
Đáp án đúng là: B
Kẻ tại H.
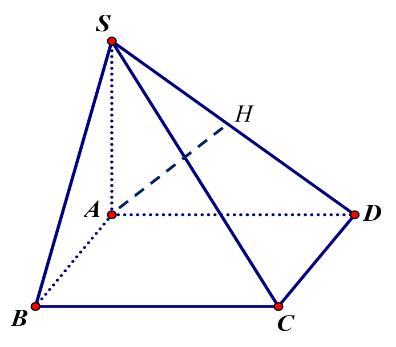
Dễ thấy .
Mà Þ .
Suy ra .
Áp dụng hệ thức lượng trong có:
.
Vậy .
Nhà sách VIETJACK:
🔥 Đề thi HOT:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
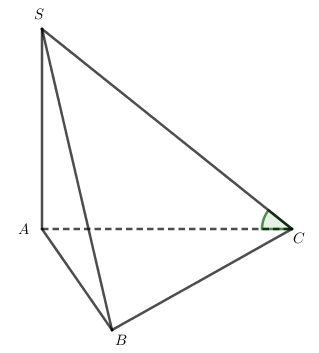
Cho hình chóp S.ABC có ; tam giác ABC đều cạnh a và SA = a. Tìm góc giữa SC và mặt phẳng (ABC).
Câu 2:
Tập nghiệm của bất phương trình là
Câu 3:
Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức z thỏa mãn là một đường tròn. Tâm của đường tròn đó có tọa độ là
Câu 4:
Cho hàm số có đồ thi là đường cong trong hình bên.
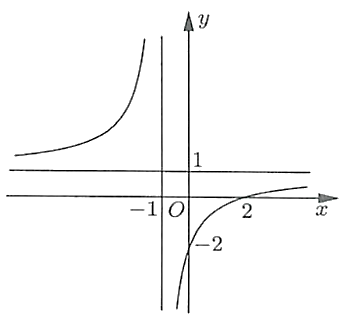
Toạ độ giao điểm của đồ thị hàm số đã cho và trục tung là:
Câu 5:
Trong không gian Oxyz, góc giữa hai mặt phẳng (Oxy) và (Oyz) bằng
Câu 6:
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng
