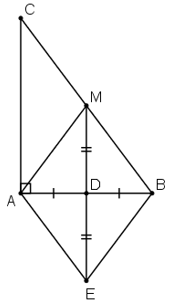
a) Ta sở hữu MB = MC, DB = DA
⇒ MD là lối khoảng của ΔABC
⇒ MD // AC
Mà AC ⊥ AB
⇒ MD ⊥ AB.
Mà D là trung điểm ME
⇒ AB là lối trung trực của ME
⇒ E đối xứng với M qua quýt AB.
b) + MD là lối khoảng của ΔABC
⇒ AC = 2MD.
E đối xứng với M qua quýt D
⇒ D là trung điểm EM
⇒ EM = 2.MD
⇒ AC = EM.
Lại sở hữu AC // EM
⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì thế sở hữu những lối chéo cánh tách nhau bên trên trung điểm của từng lối.
Hình bình hành AEBM lại sở hữu AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
Chu vi hình thoi AEBM vì chưng 4.BM = 4.2 = 8cm
d)- Cách 1:
Hình thoi AEBM là hình vuông vắn ⇔ AB = EM ⇔ AB = AC
Vậy nếu như ABC vuông được thêm ĐK AB = AC (tức tam giác ABC vuông cân nặng bên trên A) thì AEBM là hình vuông vắn.
- Cách 2:
Hình thoi AEBM là hình vuông vắn ⇔ AM ⊥ BM
⇔ ΔABC sở hữu trung tuyến AM là lối cao
⇔ ΔABC cân nặng bên trên A.
Vậy nếu như ΔABC vuông được thêm ĐK cân nặng bên trên A thì AEBM là hình vuông vắn.
Câu 2:
Cho tứ giác ABCD. Gọi E, F, G, H bám theo trật tự là trung điểm của AB, BC, CD, DA. Các lối chéo cánh AC, BD của tứ giác ABCD sở hữu ĐK gì thì EFGH là:
a) Hình chữ nhật?
b) Hình thoi?
c) Hình vuông?