Cho tứ diện đều ABCD (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa

*Lời giải

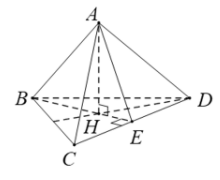
Gọi H là tâm lối tròn xoe nước ngoài tiếp $\Delta BCD\Rightarrow AH\perp \left(BCD\right)$.

Gọi E là trung điểm CD $\Rightarrow BE\perp CD$ (do $\Delta BCD$ đều).

Do $AH\perp \left(BCD\right)\Rightarrow AH\perp CD$.

Ta có: $\left\{\begin{array}{l}CD\perp BE\\ CD\perp AH\end{array}\right.\Rightarrow CD\perp \left(ABE\right)$

$\Rightarrow CD\perp AB\Rightarrow \widehat{\left(AB,CD\right)}=90°$

^*Phương pháp giải

Sử dụng đường thẳng liền mạch vuông góc với mặt mũi phẳng lì suy đi ra 2 đường thẳng liền mạch vuông góc suy đi ra góc cần thiết tìm

*Lý thuyến cần thiết cầm về góc thân thiết nhì mặt mũi phẳng: 

1. Góc thân thiết hai tuyến đường trực tiếp là gì?

- Góc thân thiết hai tuyến đường trực tiếp là góc $\alpha$ được tạo nên bởi vì hai tuyến đường trực tiếp d và d’ với số đo $0^o\le \alpha \le {90}^o$. Khi d tuy vậy song hoặc trùng với d’, tao quy ước góc thân thiết bọn chúng bằng $0^o$.

- Góc thân thiết hai tuyến đường trực tiếp bởi vì góc thân thiết nhì vectơ chỉ phương hoặc nhì vectơ pháp tuyến của bọn chúng.

2. Cách xác lập góc thân thiết hai tuyến đường thẳng

Để xác lập góc thân thiết hai tuyến đường trực tiếp a và b, tao lấy điểm O nằm trong 1 trong những 2 đương trực tiếp tiếp sau đó vẽ 1 đường thẳng liền mạch trải qua O và tuy vậy song với 2 lối sót lại.

Nếu vector u là vector chỉ phương của đường thẳng liền mạch a, đôi khi vector v là vector chỉ phương của đường thẳng liền mạch b, góc thân thiết (u, v) = $\alpha$ thì tao rất có thể suy đi ra góc thân thiết 2 đường thẳng liền mạch a và b bằng $\alpha$ ($0°\le \alpha \le 90°$)

- Cho hai tuyến đường trực tiếp d và d’ có vectơ chỉ phương lần lượt là: $\overrightarrow{u}=(a;b)$ và $\overrightarrow{u\text{'}}=(a\text{'};b\text{'})$. Góc thân thiết hai tuyến đường trực tiếp được xác lập bởi:

$\cos (d,d\text{'})=\left|cos(\overrightarrow{u},\overrightarrow{u\text{'}})\right|=\frac{\left|a.a\text{'}+b.b\text{'}\right|}{\sqrt{a^2+b^2}.\sqrt{a{\text{'}}^2+b{\text{'}}^2}}$

- Cho hai tuyến đường trực tiếp d và d’ có vectơ pháp tuyến lần lượt là: $\overrightarrow{n}=(a;b)$ và $\overrightarrow{n\text{'}}=(a\text{'};b\text{'})$. Góc thân thiết hai tuyến đường trực tiếp được xác lập bởi:

$\cos (d,d\text{'})=\left|cos(\overrightarrow{n},\overrightarrow{n\text{'}})\right|=\frac{\left|a.a\text{'}+b.b\text{'}\right|}{\sqrt{a^2+b^2}.\sqrt{a{\text{'}}^2+b{\text{'}}^2}}$

- Gọi k và k’ theo thứ tự là thông số góc của hai tuyến đường trực tiếp d và d’. Ta có:

$\tan (d,d\text{'})=\left|\frac{k-k\text{'}}{1+k.k\text{'}}\right|$

Xem tăng những tham khảo thêm hoặc, chi tiết:

Công thức tính góc thân thiết hai tuyến đường trực tiếp (2024) những dạng bài bác tập dượt và cơ hội giải