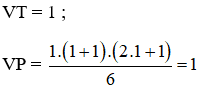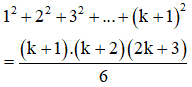Chứng minh rằng với n thuộc N*, ta có đẳng thức: 1^2 + 2^2 + 3^2 + ... + n^2 (Miễn phí)

20,000

Tác giả: admin

Ngày đăng: 11:45 18/12/2024

Tình trạng: Còn hàng

Câu hỏi:

13/07/2024 58,801

Chứng minh rằng với n ∈ N*, tớ đem đẳng thức: $1^{2} + 2^{2} + 3^{2} + . . . . + n^{2} = \frac{n (n + 1) (2 n + 1)}{6}$

+ Với n = 1 :

Giải bài xích 1 trang 82 sgk Đại số 11 | Để học tập chất lượng Toán 11

⇒ (3) đích thị với n = 1

+ Giả sử đẳng thức (3) đích thị với n = k tức là :

Giải bài tập Đại số 11 | Để học tập chất lượng Toán 11

Cần chứng tỏ (3) đúng vào khi n = k + 1, tức là:

Giải bài xích 1 trang 82 sgk Đại số 11 | Để học tập chất lượng Toán 11

Thật vậy:

Giải bài xích 1 trang 82 sgk Đại số 11 | Để học tập chất lượng Toán 11

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Chứng minh rằng với $n \in N *$ thì $1 + 2 + 3 + . . . + n = \frac{n (n + 1)}{2}$

Câu 2:

Chứng minh rằng với $n \in N * : n^{3} + 11 n$ phân chia không còn cho tới 6.

Câu 3:

cho tổng $S_{n} = \frac{1}{1.2} + \frac{1}{2.3} + . . . + \frac{1}{n (n + 1)}$ với $n \in N *$

a.Tính S1, S2, S3

b.Dự đoán công thức tính tổng Sn và chứng tỏ vì chưng quy hấp thụ.

Câu 4:

Chứng minh rằng với $n \in N *$ , tớ đem đẳng thức: $2 + 5 + 8 + . . . + 3 n - 1 = \frac{n (3 n + 1)}{2}$

Câu 5:

Chứng minh rằng với $n \in N * : 4^{n} + 15 n - 1$ phân chia không còn cho tới 9

Câu 6:

Chứng minh rằng số đàng chéo cánh của một nhiều giác lồi n cạnh là $n (n - 3) / 2$