Trong những dạng toán tính độ quý hiếm biểu thức hoặc tính thời gian nhanh, tất cả chúng ta tiếp tục thấy một trong những Việc tính tổng mặt hàng số (dãy số liên tục, mặt hàng số cơ hội đều,…). Phương pháp thực hiện những dạng này thiệt đi ra vô cùng đơn giản và giản dị, hãy cũng tương tự như MATHX tò mò nhé!
Công thức tính tổng những mặt hàng số hạng liên tiếp

Tính tổng S(n) = 1 + 2 + 3 + … + n –
Ví dụ 1: Tính tổng: S = 1 + 2 + 3 + 4 + 5 + ... + 97 + 98 + 99
Phân tích và giải:
Ta thấy tổng S có thể tính theo đòi 2 cách (từ đầu đến cuối hoặc từ cuối lên đầu)
S = 1 + 2 + 3 + ... + 97 + 98 + 99
S = 99 + 98 + 97 + ... + 3 + 2 + 1
Ta cộng lại:
S + S = (1 + 99) + (2 + 98) + (3 + 97) + ... + (97 + 3) + (98 + 2) + (99 + 1)
S x 2 = (1 + 99) x 99
S = (1 + 99) x 99 : 2 = 2950
Ta có thể xây dựng công thức tổng quát để tìm tổng các số hạng của một dãy số ngẫu nhiên liên tục như sau:
Tổng = (số đầu + số cuối) x số số hạng : 2
Ví dụ 2: Tính tổng: S = 1 + 3 + 5 + 7 + ...+ 95 + 97 + 99
Phân tích và giải:
Cũng tương tự như ví dụ 1, tao sẽ tính như sau:
S = 1 + 3 + 5 + ... + 95 + 97 + 99
S = 99 + 97 + 95 + ... 5 + 3 + 1
S + S = (1 + 99) + (3 + 97) + (5 + 95) + ... + (95 + 5) + (97 + 3) + (99 + 1)
Vấn đề để đi ra lúc này là cần tìm coi có từng nào nhóm có tổng bằng 100 ở bên trên. Số nhóm này chính là số số hạng của dãy số 1, 3, 5, ..., 99
Ta sở hữu công thức tính số số hạng của mặt hàng số cơ hội đều:
Số số hạng = (Số cuối – Số đầu) : Khoảng cơ hội + 1
Ta có số số hạng là: (99 – 1) : 2 + 1 = 50 (số hạng)
Từ đó tính được tổng:
S = (1 + 99) x 50 : 2 = 2500.
Liên quan liêu cho tới mặt hàng số cơ hội đều còn tồn tại dạng lần số hạng loại n của mặt hàng số cơ hội đều.
Các con cái hoàn toàn có thể xem thêm tăng tại: TÌM SỐ HẠNG THỨ N CỦA DÃY SỐ CÁCH ĐỀU
Bây giờ tất cả chúng ta nằm trong ôn tập luyện tăng một trong những Việc về dạng này nhé!
Bài 1. Tính tổng: S = 1 + 2 + 3 + ... + 29
Lời giải:
Tổng mặt hàng số bên trên là:
( 29 + 1 ) x 29 : 2 = 435
Đáp số: 435
Bài 2. Tính tổng S = 2 + 4 + 6 + ... + 18 + 40
Lời giải:
Số những số hạng của mặt hàng số bên trên là:
( 40 – 2 ) : 2 + 1 = đôi mươi (số hạng)
Tổng mặt hàng số bên trên là:
( 40 + 2 ) x đôi mươi : 2 = 420
Đáp số: 420
Bài 3. Cho dãy số: 1, 3, 5, 7, ..., 59. Tính tổng các số hạng của dãy số bên trên.
Lời giải:
Số những số hạng của mặt hàng số bên trên là:
( 59 – 1 ) : 2 + 1 = 30 (số hạng)
Tổng mặt hàng số bên trên là:
( 59 + 1 ) x 30 : 2 = 900
Đáp số: 900
Bài 4. Hình thứ đôi mươi theo đòi quy luật dưới phía trên gồm từng nào dù vuông trắng?
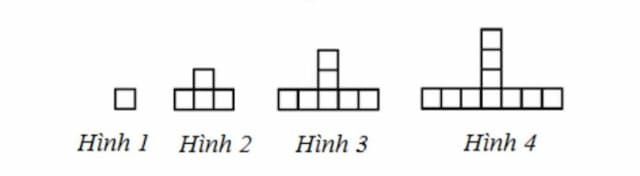
Tìm dù vuông Trắng ở hình loại 20
Lời giải:
Hình 1 có một dù vuông trắng
Hình 2 có một + 2 = 3 dù vuông trắng
Hình 3 có một + 2 + 3 = 6 dù vuông trắng
Hình 4 có một + 2 + 3 + 4 = 10 dù vuông trắng
Hình loại đôi mươi có một + 2 + 3 + 4 + … + 19 + đôi mươi = (20 + 1) x đôi mươi : 2 = 210 dù vuông Trắng.
