Câu hỏi:
12/07/2024 1,236
Để sửa một căn nhà cần thiết một số trong những công nhân thao tác làm việc nhập một thời hạn quy toan. Nếu hạn chế tía người thì thời hạn kéo dãn sáu ngày. Nếu gia tăng nhị người thì đoạn sớm nhị ngày. Hỏi theo đòi quy toan cần thiết từng nào công nhân và thực hiện nhập từng nào ngày. thạo rằng tài năng làm việc của từng công nhân đều như nhau?
Trả lời:
![]()
Giải bởi Vietjack
Gọi số công nhân quan trọng là x (người), x ∈ ℕ* , thời hạn quan trọng là hắn (ngày), hắn > 0.
Số ngày công cần thiết nhằm hoàn thiện việc làm là: xy (ngày).
Nếu giảm xuống 3 người thì thời hạn kéo dãn 6 ngày. Như vậy, x – 3 người thực hiện nhập hắn + 6 ngày thì đoạn việc làm. Do ê, tớ với phương trình (x – 3)(y + 6) = xy.
Nếu gia tăng 2 người thì đoạn sớm 2 ngày. Như vậy, x + 2 người thực hiện nhập hắn – 2 ngày thì đoạn việc làm. Do ê, tớ với phương trình: (x + 2)(y – 2) = xy.
Ta với hệ phương trình:
Vậy cần thiết 8 người thực hiện nhập 10 ngày thì đoạn việc làm.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC với AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh nhị tam giác ABM và ACM đều nhau.
b) Chứng minh AM vuông góc với BC.
c) Chứng minh AM là phân giác của góc A.
Cho tam giác ABC với AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh nhị tam giác ABM và ACM đều nhau.
b) Chứng minh AM vuông góc với BC.
c) Chứng minh AM là phân giác của góc A.
Câu 2:
Chứng minh những hệ thức:
a) ;
b) .
Chứng minh những hệ thức:
a) ;
b) .
Câu 3:
Một người đứng bên trên tháp để ý của ngọn đèn biển cao 50 m nom về phía Tây Nam, người ê để ý nhị phen một chiến thuyền đang được thiên về ngọn đèn biển. Lần loại nhất người ê bắt gặp thuyền với góc hạ là 20°, phen thứ hai người ê bắt gặp thuyền với góc hạ là 30°. Hỏi chiến thuyền đã từng đi được từng nào mét thân thuộc nhị phen quan liêu sát? (làm tròn trĩnh cho tới chữ số thập phân loại nhất)
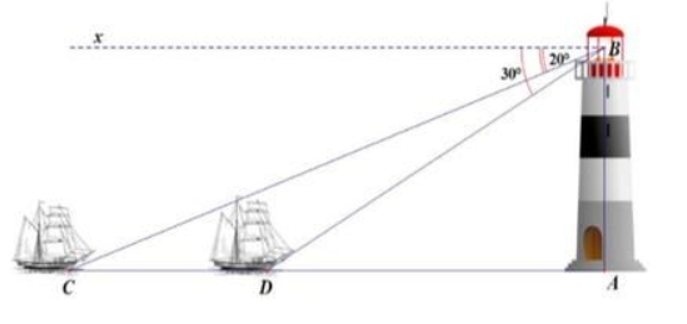
Một người đứng bên trên tháp để ý của ngọn đèn biển cao 50 m nom về phía Tây Nam, người ê để ý nhị phen một chiến thuyền đang được thiên về ngọn đèn biển. Lần loại nhất người ê bắt gặp thuyền với góc hạ là 20°, phen thứ hai người ê bắt gặp thuyền với góc hạ là 30°. Hỏi chiến thuyền đã từng đi được từng nào mét thân thuộc nhị phen quan liêu sát? (làm tròn trĩnh cho tới chữ số thập phân loại nhất)

Câu 4:
Một mảnh đất nền hình chữ nhật bị xén chuồn một góc (hình vẽ), phần còn sót lại với hình trạng tứ giác ABCD với phỏng nhiều năm những cạnh là AB = 15m, BC = 19m, CD = 10m, DA = 20m. Diện tích mảnh đất nền ABCD bởi từng nào mét vuông (làm tròn trĩnh sản phẩm cho tới sản phẩm đơn vị).
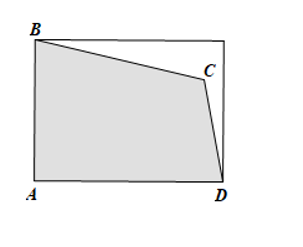
Một mảnh đất nền hình chữ nhật bị xén chuồn một góc (hình vẽ), phần còn sót lại với hình trạng tứ giác ABCD với phỏng nhiều năm những cạnh là AB = 15m, BC = 19m, CD = 10m, DA = 20m. Diện tích mảnh đất nền ABCD bởi từng nào mét vuông (làm tròn trĩnh sản phẩm cho tới sản phẩm đơn vị).

Câu 5:
Cho (O), điểm A ở phía bên ngoài đàng tròn trĩnh. Vẽ những tiếp tuyến AB, AC và cát tuyến ADE. Gọi H là trung điểm của DE.
a) Chứng minh 5 điểm A, B, H, O, C nằm trong phụ thuộc 1 đàng tròn trĩnh.
b) Chứng minh HA là tia phân giác của góc BHC.
c) Gọi I là phú của BC và DE. Chứng minh AB2 = AI.AH.
d) BH hạn chế (O) ở K. Chứng minh AE // CK.
Cho (O), điểm A ở phía bên ngoài đàng tròn trĩnh. Vẽ những tiếp tuyến AB, AC và cát tuyến ADE. Gọi H là trung điểm của DE.
a) Chứng minh 5 điểm A, B, H, O, C nằm trong phụ thuộc 1 đàng tròn trĩnh.
b) Chứng minh HA là tia phân giác của góc BHC.
c) Gọi I là phú của BC và DE. Chứng minh AB2 = AI.AH.
d) BH hạn chế (O) ở K. Chứng minh AE // CK.
Câu 6:
Cho đàng tròn trĩnh (O; R) và điểm A cố định và thắt chặt ngoài đàng tròn trĩnh. Vẽ đường thẳng liền mạch d vuông góc với OA bên trên A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF hạn chế OM bên trên H, hạn chế OA bên trên B.
a) Chứng minh tứ giác ABHM nội tiếp.
b) Chứng minh OA.OB = OH.OM = R2.
c) Chứng minh tâm I của đàng tròn trĩnh nội tiếp tam giác MEF nằm trong một đàng tròn trĩnh cố định và thắt chặt khi M dịch chuyển bên trên d.
d) Tìm địa điểm của M nhằm diện tích S tam giác HBO lớn số 1.
Cho đàng tròn trĩnh (O; R) và điểm A cố định và thắt chặt ngoài đàng tròn trĩnh. Vẽ đường thẳng liền mạch d vuông góc với OA bên trên A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF hạn chế OM bên trên H, hạn chế OA bên trên B.
a) Chứng minh tứ giác ABHM nội tiếp.
b) Chứng minh OA.OB = OH.OM = R2.
c) Chứng minh tâm I của đàng tròn trĩnh nội tiếp tam giác MEF nằm trong một đàng tròn trĩnh cố định và thắt chặt khi M dịch chuyển bên trên d.
d) Tìm địa điểm của M nhằm diện tích S tam giác HBO lớn số 1.
Câu 7:
Cho đàng tròn trĩnh (O) chạc cung BC (BC ko là đàng kính). Điểm A địa hình bên trên cung nhỏ BC (A không giống B và C, phỏng nhiều năm cạnh AB không giống AC). Kẻ 2 lần bán kính AA' của đàng tròn trĩnh (O), D là chân đàng vuông góc kẻ kể từ A cho tới BC. Hai điểm E, F theo lần lượt là chân đàng vuông góc kẻ kể từ B, C cho tới AA'.
a) Chứng minh rằng 4 điểm A, B, D, E nằm trong phía trên 1 đàng tròn trĩnh.
b) Chứng minh BD.AC = AD.A'C.
Cho đàng tròn trĩnh (O) chạc cung BC (BC ko là đàng kính). Điểm A địa hình bên trên cung nhỏ BC (A không giống B và C, phỏng nhiều năm cạnh AB không giống AC). Kẻ 2 lần bán kính AA' của đàng tròn trĩnh (O), D là chân đàng vuông góc kẻ kể từ A cho tới BC. Hai điểm E, F theo lần lượt là chân đàng vuông góc kẻ kể từ B, C cho tới AA'.
a) Chứng minh rằng 4 điểm A, B, D, E nằm trong phía trên 1 đàng tròn trĩnh.
b) Chứng minh BD.AC = AD.A'C.
Bình luận
Hãy Đăng nhập hoặc Tạo thông tin tài khoản nhằm gửi comment
Bình luận
