Vietjack.bủ reviews cỗ thắc mắc ôn tập dượt Toán sở hữu đáp án được biên soạn bám sát công tác học tập khiến cho bạn ôn luyện và bổ sung cập nhật kiến thức và kỹ năng môn Toán đảm bảo chất lượng rộng lớn. Mời chúng ta đón xem:
Lớp 10A sở hữu 10 học viên xuất sắc Toán, 10 học viên xuất sắc Lý, 11 học viên xuất sắc Hóa
Đề bài: Lớp 10A sở hữu 10 học viên xuất sắc Toán, 10 học viên xuất sắc Lý, 11 học viên xuất sắc Hóa, 6 học viên xuất sắc cả Toán và Lý, 5 học viên xuất sắc cả Hóa và Lý, 4 học viên xuất sắc cả Toán và Hóa, 3 học viên xuất sắc cả thân phụ môn Toán, Lý, Hóa. Số học viên xuất sắc tối thiểu 1 trong những thân phụ môn (Toán, Lý, Hóa) của lớp 10A là:
A. 19
B. 18
C. 31
D. 49
Đáp án chính A
* Lời giải:
Theo fake thiết Đề bài mang đến, tao sở hữu biểu trang bị Ven:
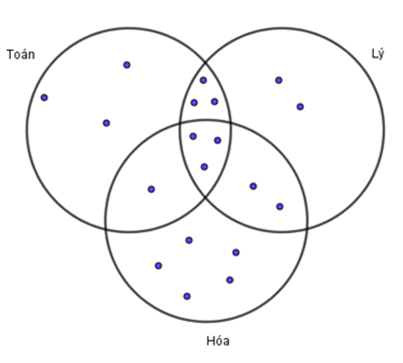
Dựa vô biểu trang bị Ven tao thấy:
Số học viên chỉ xuất sắc Toán và Lý (không xuất sắc Hóa) là: 6 – 3 = 3 (em)
Số học viên chỉ xuất sắc Toán và Hóa (không xuất sắc Lý) là: 4 – 3 = 1 (em)
Số học viên chỉ xuất sắc Lý và Hóa (không xuất sắc Toán) là: 5 – 3 = 2 (em)
Số học viên chỉ xuất sắc một môn Toán là: 10 – 3 – 3 – 1 = 3 (em)
Số học viên chỉ xuất sắc một môn Lý là: 10 – 3 – 3 – 2 = 2 (em)
Số học viên chỉ xuất sắc một môn Hóa là: 11 – 1 – 3 – 2 = 5 (em)
Số học viên xuất sắc tối thiểu 1 trong những thân phụ môn là:
3 + 2 + 5 + 1 + 2 + 3 + 3 = 19 (em)
* Phương pháp giải:
Sử dụng sơ trang bị Ven nhằm minh họa những tụ tập.
Dựa vô sơ trang bị Ven tao thiết lập được đẳng thức hoặc phương trình kể từ bại liệt tìm kiếm ra thành quả vấn đề.
* Lý thuyết cần thiết bắt và dạng toán về mệnh đề và tập dượt hợp:
Gồm 3 bước:
+ Bước 1: Chuyển vấn đề về ngữ điệu tụ tập.
+ Bước 2: Sử dụng sơ trang bị Ven nhằm minh họa những tụ tập.
+ Bước 3: Dựa vô sơ trang bị Ven tao thiết lập được đẳng thức hoặc phương trình, hệ phương trình, kể từ bại liệt tìm kiếm ra thành quả vấn đề.
Các tập dượt con cái thông thường sử dụng của ℝ
- Một số tập dượt con cái thông thường sử dụng của tập dượt số thực ℝ:
+ Khoảng:




+ Đoạn

+ Nửa khoảng




- Kí hiệu + ∞: Đọc là dương vô đặc biệt (hoặc dương vô cùng).
- Kí hiệu – ∞: Đọc là âm vô đặc biệt (hoặc âm vô cùng).
- a, b gọi là những đầu mút của đoạn, khoảng tầm hoặc nửa khoảng tầm.
Giao của nhì tập dượt hợp
Tập thích hợp bao gồm những thành phần nằm trong cả nhì tụ tập S và T gọi là giao của nhì tập dượt hợp S và T, kí hiệu là S ∩ T.
S ∩ T ={x | x ∈ S và x ∈ T}.
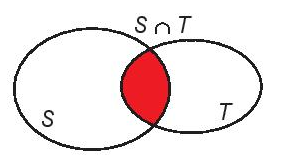
Hợp của nhì tập dượt hợp
- Tập thích hợp bao gồm những thành phần nằm trong tụ tập S hoặc nằm trong tụ tập T gọi là hợp của nhì tập dượt hợp S và T, kí hiệu là S ∪ T.
S ∪ T = {x | x ∈ S hoặc x ∈ T}.
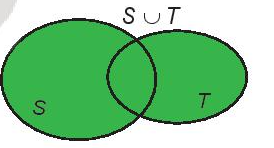
Hiệu của nhì tập dượt hợp
- Hiệu của nhì tập dượt hợp S và T là tụ tập bao gồm những thành phần nằm trong S tuy nhiên ko nằm trong T, kí hiệu là S \ T.
S \ T = {x | x ∈ S và x ∉ T}.
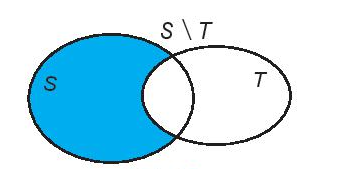
- Nếu T ⊂ S thì S \ T được gọi là phần bù của T vô S, kí hiệu CST.
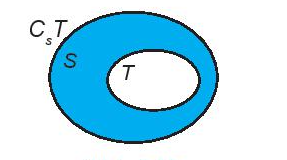
Chú ý: .
Xem tăng những xem thêm hoặc, chi tiết
Tổng phù hợp thuyết Chương 1 - Toán 10 Kết nối tri thức
TOP 30 câu Trắc nghiệm Ôn tập dượt cuối chương 1 (Kết nối trí thức 2024) sở hữu đáp án - Toán 10
Xem tăng những thắc mắc ôn tập dượt Toán chọn thanh lọc, hoặc khác:
Từ những chữ số: 1, 2, 3, 4, 5, 6, 7. Hỏi rất có thể lập được từng nào số sở hữu 6 chữ số...
Từ những số của tập dượt A = {1; 2; 3; 4; 5; 6; 7} lập được từng nào số ngẫu nhiên bao gồm...
Cho tam giác ABC vuông bên trên A, sở hữu AB < AC, bên trên cạnh BC lấy điểm D...
Cho tam giác ABC vuông góc bên trên A,sở hữu AB = AC.Gọi K là trung điểm của cạnh BC...
Lớp 10A sở hữu 10 học viên xuất sắc Toán, 10 học viên xuất sắc Lý, 11 học viên xuất sắc Hóa...
Lớp 10A sở hữu 7 học viên xuất sắc Toán, 5 học viên xuất sắc Lý, 6 học viên xuất sắc Hoá...
Cho tam giác ABC. Có AB nhỏ rộng lớn AC bên trên cạnh AB lấy điểm E sao mang đến...
Cho tam giác ABC . Trên những cạnh AB và AC thứu tự lấy nhì điểm D và E...
Nêu định nghĩa hình chiếu? Cho ví dụ và phân tách...
Cho tam giác ABC cố định và thắt chặt (AB < AC). Hai điểm D, E theo đòi trật tự vận động...
Cho 4 điểm phân biệt A, B, C, D. Có từng nào vectơ không giống vectơ – ko....
Trong không khí mang đến 4 điểm A,B,C,D. Từ những điểm bên trên tao rất có thể lập được...
3−5−3+5. Tính và rút gọn gàng...
3−5−3-5. Tính và rút gọn gàng...
Cho tam giác ABC vuông bên trên A gọi M là trung điểm BC biết BC...
Cho tam giác ABC vuông bên trên A sở hữu M là trung điểm của BC...
Cho tụ tập A = {0; 1; 2; 3; 4; 5}. cũng có thể lập từng nào số ngẫu nhiên chẵn...
Với những chữ số 0, 1, 2, 3, 4, 5 rất có thể lập được từng nào số ngẫu nhiên chẵn...
Cho tứ giác ABCD. Gọi M, N, P.., Q thứu tự là trung điểm AB, BC, CD, DA...
Cho tứ giác ABCD sở hữu M , N , P.. , Q thứu tự là trung điểm của AB , BC...
Cho những số 0;1;2;3;4;5;6;7. Từ những chữ số bên trên lập được từng nào số sở hữu 4 chữ số...
Số những số sở hữu 4 chữ số song một không giống nhau được tạo ra trở nên kể từ những chữ số 2, 4, 6, 7, 8, 9 là...
Một nông trại cân nặng mượn xe vận đem 450 con cái heo và 35 tấn cám...
Chứng minh rằng: D = 1 + 4 + 42 + 42 + ... + 458 + 459 phân tách không còn mang đến 21...
Cho A = 1 + 4 + 42 + 43 +...+ 411. Chứng tỏ rằng...
Người tao sử dụng bao nhiêu hình chiếu nhằm màn trình diễn khối tròn xoe xoay...
x2 – 16 + 4y2 + 4xy. Phân tích nhiều thức trở nên nhân tử...
Phân tích nhiều thức trở nên nhân tử 16 - x² - 4xy - 4y²...
Cho tam giác ABC vuông bên trên A, đàng cao AH. Gọi E, F thứu tự là...
Một gương phẳng phiu hình tròn trụ 2 lần bán kính 10 centimet bịa đặt bên trên bàn cơ hội xà nhà 2m...
Cho tam giác ABC. Tìm tụ tập những điểm M sao mang đến...
Cho DABC. Tìm tụ tập điểm M trong những tình huống sau...
Giải phương trình: căn (x^2 + x + 1)...
Phân tích nhiều thức x^4 + 2x^3 – 4x – 4 trở nên nhân tử...
Trong không khí Oxyz, phương trình mặt mũi phẳng phiu (P) chứa chấp trục Ox và vuông góc...
Đạo hàm của hàm số hắn = (3 - x^2)^ 2/3...
Một hình chữ nhật sở hữu chiều lâu năm là 12m, chiều rộng lớn là 8m. một hình vuông vắn sở hữu chu vi...
Chứng minh với a, b, c ∈ ℝ tao có: (a + b + c)^2. (ab + bc + ca)^2 ≥ 3(ab + bc + ca)^3...
Giải phương trình sin 2x + cos (6x + pi/3) = 0...
Giải phương trình 2sin2x + căn 2 sin 4x = 0...
Tìm độ quý hiếm nhỏ nhất của biểu thức A = 3x^2 – 2x + 1...
Cho A = [m; m + 1] và B = (-1; 3). Tìm ĐK nhằm A ∩ B = Ø...
Phân tích x^2 – 5x + 6 trở nên nhân tử...
Từ những chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9, rất có thể lập được từng nào số ngẫu nhiên sở hữu 4 chữ số...
Bán kính đàng tròn xoe nội tiếp tam giác đều cạnh a vì chưng...
Chứng minh P(n) = n^4 – 14n^3 + 71n^2 – 154n + 120 phân tách không còn mang đến 24...
Một group sở hữu 5 nam giới và 3 phái đẹp. Chọn đi ra 3 người sao mang đến vô bại liệt sở hữu tối thiểu 1 phái đẹp...
Một group học viên bao gồm 5 nam giới và 3 phái đẹp. Có từng nào cơ hội lựa chọn 5 người...
Tìm x biết 3x + 5 phân tách không còn mang đến x – 1...
