Đề bài
Một cầu trượt vô khu vui chơi công viên có tính dốc là ${28^0}$ và có tính cao là $2,1m.$Tính chừng lâu năm của mặt mày cầu trượt (làm tròn trặn cho tới chữ số thập phân loại hai).
-
A.
$3,95\,m$
-
B.
$3,8\,m$
-
C.
$4,5\,m$
-
D.
$4,47\,m$
Lời giải của GV Loigiaihay.com
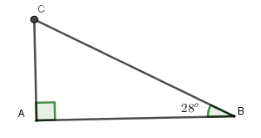
Ta có tính lâu năm của mặt mày cầu trượt là $AB$; $AC = 2,1\,m$ và $\widehat {ABC} = 28^\circ $
Xét tam giác $ACB$ vuông bên trên $A$ có
$BC = AB:\sin B = 2,1:\sin 28^\circ \simeq 4,47\,m$
Vậy chừng lâu năm của mặt mày cầu trượt là $4,47\,m.$
Đáp án : D

Các bài bác luyện nằm trong thường xuyên đề
Bài 1 :Một cột đèn với bóng bên trên mặt mày khu đất lâu năm $7,5m.$ Các tia nắng nóng mặt mày trời tạo ra với mặt mày khu đất một góc xấp xỉ vì chưng ${42^0}.$ Tính độ cao của cột đèn. (làm tròn trặn cho tới chữ số thập phân loại ba) Xem tiếng giải >> Bài 2 :Hai điểm P.. và Q xa nhau 203 m và trực tiếp mặt hàng với chân một tòa tháp (Hình 3). Từ đỉnh của tòa tháp cơ, một người phát hiện ra nhì điểm P.., Q với nhì góc nghiêng xuống theo thứ tự là \({38^o}\) và \({44^o}\). Tính độ cao của tòa tháp (kết trái ngược thực hiện tròn trặn cho tới mặt hàng đơn vị chức năng của mét). Xem tiếng giải >> Bài 3 :Mặt rời đứng của khuông thép với dạng tam giác cân nặng \(ABC\) với \(\widehat B = 23^\circ ,AB = 4m\) (Hình 33). Tính chừng lâu năm đoạn trực tiếp \(BC\) (làm tròn trặn thành quả cho tới mặt hàng phần chục của mét). Xem tiếng giải >> Bài 4 :Để ước tính độ cao của một cây vô Sảnh ngôi trường, chúng ta Hoàng đứng ở Sảnh ngôi trường (theo phương trực tiếp đứng), mặt mày chúng ta Hoàng bịa bên trên địa điểm \(C\) cơ hội mặt mày khu đất một khoảng chừng \(CB = DH = 1,64m\) và cơ hội cây một khoảng chừng \(CD = BH = 6m\). Tính độ cao \(AH\) của cây (làm tròn trặn thành quả cho tới mặt hàng Xác Suất của mét), biết tầm nhìn \(ACD\) vì chưng \(38^\circ \) minh họa ở Hình 36. Xem tiếng giải >> Bài 5 :Trên mặt mày biển lớn, Lúc khoảng cách \(AB\) kể từ ca nô cho tới chân tháp đèn biển là 250m, một người đứng bên trên tháp đèn biển cơ quan sát về phía ca nô bám theo phương \(CA\) tạo ra với phương ở ngang \(Cx\) một góc là \(\widehat {ACx} = 32^\circ \) (Hình 39). Tính độ cao của tháp đèn biển (làm tròn trặn thành quả cho tới mặt hàng phần chục của mét), biết \(AB//Cx\) và chừng cao kể từ tầm đôi mắt của những người cơ cho tới đỉnh tháp là 3,2m. Xem tiếng giải >> Bài 6 :Người tớ kể lại rằng, vô thế kỉ XVI, ngôi nhà khoa học tập Galileo vẫn thả rơi những trái ngược cầu nằm trong thể tích kể từ tháp nghiêng Pisa xuống mặt mày khu đất. Ông vạc hình thành hiện tượng kỳ lạ lí thú rằng thời hạn một vật rơi tự tại ko tùy thuộc vào trọng lượng của vật cơ (nguồn: https://www.britannica.com/summary/Galileo-Timeline). hiểu độ cao của tháp nghiêng Pisa ở phía thấp rộng lớn là \(AH = 55,9m\) và góc nghiêng BAH của tháp đối với phương trực tiếp đứng là khoảng chừng \({4^o}\) (Hình 4.25), nếu như thả một trái ngược bóng từ vựng trí A bên trên đỉnh tháp xuống khu đất thì bóng tiếp tục vấp khu đất cơ hội điểm B ở chân tháp là từng nào mét? Xem tiếng giải >> Bài 7 :Cánh tay rô-bốt bịa bên trên mặt mày khu đất và nằm tại như Hình 4.28. Tính chừng cao của điểm A bên trên đầu cánh tay rô-bốt đối với mặt mày khu đất. Xem tiếng giải >> Bài 8 :Làm tròn trặn số đo góc cho tới phút và chừng lâu năm cho tới mặt hàng phần chục của đơn vị chức năng đo chừng lâu năm được cho tới. Trong Hình 4.29, một cánh diều được thả bên trên khung trời với chiều lâu năm chạc là \(AD = 150m\), góc tạo ra vì chưng chạc diều và phương ở ngang là \(\widehat {DAH} = {40^o}\). Tính chừng cao DH của cánh diều đối với mặt mày khu đất. Xem tiếng giải >> Bài 9 :Làm tròn trặn số đo góc cho tới phút và chừng lâu năm cho tới mặt hàng phần chục của đơn vị chức năng đo chừng lâu năm được cho tới. Khi tia sáng sủa được truyền qua quýt mặt mày phân cơ hội thân mật bầu không khí và nước thì lối đi tia sáng sủa có khả năng sẽ bị chéo lên đường vì thế hiện tượng kỳ lạ khúc xạ khả năng chiếu sáng. Góc cho tới i và góc khúc xạ r như Hình 4.33 tương tác cùng nhau bám theo công thức \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\). Một loài cá tập bơi ở địa điểm C. Do khả năng chiếu sáng bị khúc xạ nên Minh đứng bên trên bờ coi xuống nước với góc \(r = {54^o}\) thì thấy loài cá ở địa điểm A trực tiếp mặt hàng với O, M và cơ hội mặt mày nước một quãng \(AB = 71cm\). a) Tính góc cho tới i. b) Tính chừng thâm thúy BC kể từ mặt mày nước cho tới địa điểm thực sự nhưng mà loài cá đang được tập bơi. Xem tiếng giải >> Bài 10 :Một cột đèn với bóng bên trên mặt mày khu đất lâu năm \(6m.\) Các tia nắng nóng mặt mày trời tạo ra với mặt mày khu đất một góc xấp xỉ vì chưng \({38^0}.\) Tính độ cao của cột đèn. (làm tròn trặn cho tới chữ số thập phân loại hai) Xem tiếng giải >> Bài 11 :Một cầu trượt vô khu vui chơi công viên có tính dốc là \({25^0}\) và có tính cao là \(2,4m.\) Tính chừng lâu năm của mặt mày cầu trượt (làm tròn trặn cho tới chữ số thập phân loại hai) Xem tiếng giải >> Bài 12 :Một khuôn mẫu cây bị sét tiến công trúng thân mật cây thực hiện thân mật cây ngả xuống khu đất, tạo ra với mặt mày khu đất một góc là ${40^0}$. hiểu rằng khúc cây còn đứng cao $1\,m$ . Tính độ cao khi đầu của cây. Xem tiếng giải >> Bài 13 :Một khuôn mẫu cây bị sét tiến công trúng thân mật cây thực hiện thân mật cây ngả xuống khu đất, tạo ra với mặt mày khu đất một góc là \({35^0}\) . hiểu rằng khúc cây còn đứng cao \(1,5\,m\) . Tính độ cao khi đầu của cây. (làm tròn trặn cho tới chữ số thập phân loại nhất) Xem tiếng giải >> Bài 14 :Một cái máy cất cánh đang được cất cánh lên với véc tơ vận tốc tức thời $500\,km/h$ . Đường cất cánh lên tạo ra với phương ngang một góc ${30^0}$. Hỏi sau $1,2$ phút Tính từ lúc khi đựng cánh, máy cất cánh đạt được chừng cao là bao nhiêu? Xem tiếng giải >> Bài 15 :Một cái máy cất cánh, đang được cất cánh lên với véc tơ vận tốc tức thời \(480\,km/h\) . Đường cất cánh lên tạo ra với phương ngang một góc \({25^0}\) .Hỏi sau \(1,5\) phút Tính từ lúc khi đựng cánh, máy cất cánh đạt được chừng cao là bao nhiêu? (làm tròn trặn cho tới chữ số thập phân loại nhất) Xem tiếng giải >> Bài 16 :Hai chúng ta học viên Trung và Dũng đang được đứng ở mặt mày khu đất cân đối, xa nhau $100m$ thì phát hiện ra một cái diều ( ở vị trí $C$ thân mật nhì bạn). hiểu góc ''nâng'' để xem thấy diều ở địa điểm của Trung là ${50^0}$ và góc ''nâng'' để xem thấy diều ở địa điểm của Dũng là ${40^0}$ . Hãy tính chừng cao của diều khi cơ đối với mặt mày đất? (làm tròn trặn cho tới chữ số thập phân loại hai) Xem tiếng giải >> Bài 17 :Hai chúng ta học viên Mai và Đào đang được đứng ở mặt mày khu đất cân đối, xa nhau \(150m\) thì phát hiện ra một cái diều ( ở vị trí \(C\) thân mật nhì bạn). hiểu góc ''nâng'' để xem thấy diều ở địa điểm của Mai là \({45^0}\), góc ''nâng'' để xem thấy diều ở địa điểm của Đào là \({35^0}\) . Hãy tính chừng cao của diều khi cơ đối với mặt mày đất? (làm tròn trặn cho tới chữ số thập phân loại hai) Xem tiếng giải >> Bài 18 :Hai chúng ta học viên $A$ và $B$ đang được đứng ở mặt mày khu đất cân đối, xa nhau 80 m thì phát hiện ra một máy cất cánh trực thăng tinh chỉnh và điều khiển kể từ xa xôi (ở địa điểm $C$ phía trên tia $AB$ và $AC>AB$). hiểu góc ''nâng'' để xem thấy máy cất cánh ở địa điểm của $B$ là \(55^\circ \) góc ''nâng'' để xem thấy máy cất cánh ở địa điểm của $A$ là $40^\circ $. Hãy tính chừng cao của sản phẩm cất cánh khi cơ đối với mặt mày đất? (làm tròn trặn cho tới chữ số thập phân loại hai) Xem tiếng giải >> Bài 19 :Hai chúng ta học viên A và B đang được đứng ở mặt mày khu đất cân đối, xa nhau 60 m thì phát hiện ra một máy cất cánh trực thăng tinh chỉnh và điều khiển kể từ xa xôi ( ở địa điểm C phía trên tia AB và AC>AB). hiểu góc ''nâng'' để xem thấy máy cất cánh ở địa điểm của B là \(50^\circ \) và góc ''nâng'' để xem thấy máy cất cánh ở địa điểm của A là \(30^\circ .\) Hãy tính chừng cao của sản phẩm cất cánh khi cơ đối với mặt mày đất? (làm tròn trặn cho tới chữ số thập phân loại hai) Xem tiếng giải >> Bài trăng tròn :Tính độ cao của một ngọn núi (làm tròn trặn cho tới mét), biết bên trên nhì điểm A, B xa nhau 500m (cùng 1 phía với ngọn núi), người tớ phát hiện ra đỉnh núi với góc nắng nóng theo thứ tự là \({34^o}\) và \({38^o}\). Xem tiếng giải >> Bài 21 :Bạn Thanh đứng bên trên địa điểm \(A\) cơ hội cây thông \(6m\) và phát hiện ra ngọn của cây này bên dưới một góc vì chưng \({55^0}\) đối với phương ở ngang (như hình vẽ). hiểu khoảng cách kể từ đôi mắt của người tiêu dùng Thanh cho tới mặt mày khu đất vì chưng \(1,6m.\) Chiều cao \(BC\) của cây thông vì chưng (làm tròn trặn cho tới số thập phân loại hai): Xem tiếng giải >> Bài 22 :Bạn Đức đứng bên trên nóc ngôi nhà tại chừng cao 8 m. Vị trí đôi mắt chúng ta Đức (tại địa điểm A) cơ hội nóc ngôi nhà 1,5 m. Quý Khách phát hiện ra địa điểm B tối đa của một toà ngôi nhà với góc tạo ra vì chưng tia AB và tia AH bám theo phương ở ngang là \(\widehat {BAH} = 60^\circ \). Quý Khách Đức cũng phát hiện ra địa điểm K bên trên chân tòa ngôi nhà cơ với góc tạo ra vì chưng tia AK và tia AH là \(\widehat {HAK} = 15^\circ \), AH vuông góc với BK bên trên H (Hình 16). Tính độ cao BK của tòa ngôi nhà (làm tròn trặn thành quả cho tới mặt hàng phần chục của mét). Xem tiếng giải >> Bài 23 :Một người đứng xa xôi tòa ngôi nhà 100m, người sử dụng giác nối tiếp trực tiếp đứng phát hiện ra điểm bên trên nóc ngôi nhà với tầm nhìn \({15^o}\) (so với phương ở ngang) (H.4.13). Hỏi tòa ngôi nhà cao từng nào mét (làm tròn trặn cho tới chữ số thập phân loại nhất), biết độ cao của giác nối tiếp là 1 trong,7m? Xem tiếng giải >> Bài 24 :Cho nhì tòa ngôi nhà xa nhau 32m. Tại điểm A bên trên nóc tòa ngôi nhà cao coi xuống nóc D và chân C của tòa ngôi nhà thấp theo thứ tự bám theo những góc \({15^o}\) và \({43^o}\) (so với phương ở ngang) (H.4.16). Tính độ cao của nhì tòa ngôi nhà cơ (làm tròn trặn cho tới m). Xem tiếng giải >> Bài 25 :Một người đứng cơ hội chân ngọn đèn biển 50m, coi xuống chân đèn biển bên dưới góc \({2^o}\) và coi Tột Đỉnh ngọn đèn biển bên dưới góc \({45^o}\) (so với phương ở ngang) (H.4.22). Tính độ cao ngọn đèn biển (làm tròn trặn cho tới mét). Xem tiếng giải >> Bài 26 :Một khác nước ngoài kiểm điểm được 645 bước đi Lúc lên đường kể từ ngay lập tức bên dưới chân toàn tháp trực tiếp đi ra phía ngoài cho tới địa điểm với tầm nhìn Tột Đỉnh là 45o (Hình 9). Tính độ cao của tháp, hiểu được khoảng cách tầm của từng bước đi là 0,4 m. Xem tiếng giải >> Bài 27 :Tính độ cao của cột cờ (làm tròn trặn thành quả cho tới mặt hàng Xác Suất của mét), biết bóng của cột cờ được chiếu vì chưng khả năng chiếu sáng Mặt Trời xuống mặt mày khu đất lâu năm 10,5 m và góc tạo ra vì chưng tia sáng sủa với phương ở ngang là 36°. Xem tiếng giải >> Bài 28 :Một người đứng xin chào cờ (ở địa điểm A) cơ hội cột cờ (ở địa điểm C) với AC = trăng tròn m. Người cơ bịa đôi mắt bên trên địa điểm B cơ hội mặt mày khu đất một khoảng chừng là AB = 1,5 m. Người cơ coi Tột Đỉnh cột cờ (ở địa điểm E) bám theo phương BE tạo ra với phương ở ngang BD một góc là \(\widehat {EBD} = 32^\circ \) (Hình 20). Tính độ cao của cột cờ (làm tròn trặn thành quả cho tới mặt hàng đơn vị chức năng của mét). Xem tiếng giải >> Bài 29 :Trên mặt mày biển lớn, Lúc khoảng cách kể từ ca nô cho tới chân tháp đèn biển là AB = 300 m, một người đứng bên trên tháp đèn biển cơ, bịa đôi mắt bên trên địa điểm C và quan sát về phía ca nô bám theo phương CA tạo ra với phương ở ngang Cx một góc là \(\widehat {ACx} = 27^\circ \) (minh hoạ ở Hình 22). Tính độ cao BH của tháp đèn biển (làm tròn trặn thành quả cho tới mặt hàng Xác Suất của mét), biết AB//Cx và chừng cao kể từ tầm đôi mắt của những người cơ cho tới đỉnh tháp đèn biển là CH = 2,1 m. Xem tiếng giải >> Bài 30 :Một người (ở địa điểm A) dựng cơ hội chân núi (ở địa điểm B) là 120 m. Người này đo được góc tạo ra vì chưng phương AC và phương ở ngang là \(\widehat {BAC} = 25^\circ \) với địa điểm C là đỉnh núi. Sau cơ, người này dịch chuyển tăng 150 m đi ra phía xa xôi ngọn núi rộng lớn cho tới địa điểm D) và đo được góc tạo ra vì chưng phương DC và phương ở ngang là \(\widehat {BDC} = 25^\circ \) (Hình 32), Tính độ cao CH của ngọn núi (làm tròn trặn thành quả cho tới mặt hàng đơn vị chức năng của mét). Xem tiếng giải >>