Câu hỏi:
13/07/2024 32,978
Phương pháp:
Sử dụng hệ thức lượng nhập tam giác vuông, mong muốn tính cạnh góc vuông tao lấy cạnh huyền nhân với sin góc đối.
Cách giải:
6 phút giờ.
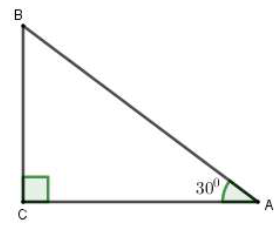
Gọi AB là đọan lối máy cất cánh bay lên nhập 6 phút thì BC đó là phỏng cao máy cất cánh đạt được sau 6 phút.
Sau 6 phút máy cất cánh bay được quãng lối là
Độ cao của dòng sản phẩm cất cánh là .
Nhà sách VIETJACK:
🔥 Đề đua HOT:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho biểu thức với
Cho x là số vẹn toàn, mò mẫm độ quý hiếm nhỏ nhất của biểu thức A.
Câu 2:
Cho hàm số (m là thông số, )
Đường trực tiếp d cắt đường thẳng liền mạch tại điểm M. Gọi N và P lần lượt là giao phó điểm của đường thẳng liền mạch và với trục hoành Ox. Tìm m để diện tích S tam giác OMP bằng 2 lần diện tích S tam giác OMN.
Cho hàm số (m là thông số, )
Đường trực tiếp d cắt đường thẳng liền mạch tại điểm M. Gọi N và P lần lượt là giao phó điểm của đường thẳng liền mạch và với trục hoành Ox. Tìm m để diện tích S tam giác OMP bằng 2 lần diện tích S tam giác OMN.
Câu 3:
Cho nửa lối tròn trặn đường kính AB. Vẽ nhì tiếp tuyến với nửa lối tròn trặn cơ. Trên tia Ax lấy điểm M sao mang lại . Từ M kẻ tiếp tuyến MC với nửa lối tròn trặn (C là tiếp điểm). Tia MC cắt tia By tại D.
Cho AM=2R. Tính BD và chu vi tứ giác ABDM
Cho nửa lối tròn trặn đường kính AB. Vẽ nhì tiếp tuyến với nửa lối tròn trặn cơ. Trên tia Ax lấy điểm M sao mang lại . Từ M kẻ tiếp tuyến MC với nửa lối tròn trặn (C là tiếp điểm). Tia MC cắt tia By tại D.
Cho AM=2R. Tính BD và chu vi tứ giác ABDM
Câu 4:
Cho hàm số (m là thông số, )
Khi m=2, hãy vẽ thiết bị thị hàm số cơ bên trên mặt mày phẳng phiu tọa phỏng Oxy và tính khoảng cách kể từ O đến đường thẳng liền mạch d.
Câu 5:
Cho nửa lối tròn trặn đường kính AB. Vẽ nhì tiếp tuyến với nửa lối tròn trặn cơ. Trên tia Ax lấy điểm M sao mang lại . Từ M kẻ tiếp tuyến MC với nửa lối tròn trặn (C là tiếp điểm). Tia MC cắt tia By tại D.
Tia AC rời tia By tại K. Chứng minh .
Cho nửa lối tròn trặn đường kính AB. Vẽ nhì tiếp tuyến với nửa lối tròn trặn cơ. Trên tia Ax lấy điểm M sao mang lại . Từ M kẻ tiếp tuyến MC với nửa lối tròn trặn (C là tiếp điểm). Tia MC cắt tia By tại D.
Tia AC rời tia By tại K. Chứng minh .
Câu 6:
Giải phương trình
