Số kilôgam thịt trườn mái ấm gia đình mua sắm là x (kg); số kilôgam thịt heo mái ấm gia đình mua sắm là hắn (kg). Vì số kilôgam thịt trườn mua sắm tối đa là một trong những,6 kilogam và số kilôgam thịt heo mua sắm tối đa là một trong những,1 kilogam nên tớ có:
0 ≤ x ≤ 1,6; 0 ≤ hắn ≤ 1,1 (1)
Vì mỗi kilôgam thịt trườn đem chứa chấp 800 đơn vị chức năng protein và mỗi kilôgam thịt lợn có chứa chấp 600 đơn vị protein nên lượng protein đem vô x kilogam thịt trườn và hắn kilogam thịt heo là: 800x + 600y (đơn vị).
Mà thường ngày mái ấm gia đình cần thiết tối thiểu 900 đơn vị chức năng protein nên tớ đem bất phương trình:
800x + 600y ≥ 900 (2)
Vì mỗi kilôgam thịt trườn đem chứa chấp 200 đơn vị lipid và mỗi kilôgam thịt lợn có chứa chấp 400 đơn vị lipid nên khối lượng lipid có vô x kilogam thịt trườn và hắn kilogam thịt heo là: 200x + 400y (đơn vị).
Mà thường ngày mái ấm gia đình cần thiết tối thiểu 400 đơn vị lipid nên tớ đem bất phương trình:
200x + 400y ≥ 400 (3)
Từ (1); (2); (3) tớ đem hệ bất phương trình:
\[\left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le hắn \le 1,1\\800x + 600y \ge 900\\200x + 400y \ge 400\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le hắn \le 1,1\\8x + 6y \ge 9\\x + 2y \ge 2\end{array} \right.\]
Ta cút xác lập miền nghiệm của hệ bất phương trình.
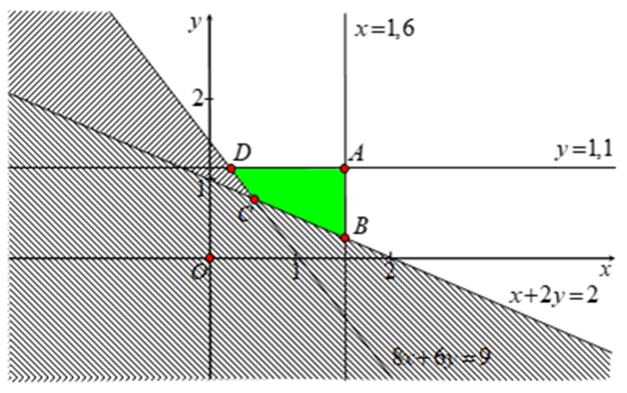
Miền nghiệm của hệ bất phương trình là tứ giác ABCD đem vô hình vẽ trên với tọa chừng những đỉnh là A(0,3; 1,1), B(0,6; 0,7), C(1,6; 0,2), D(1,6; 1,1).
b) Số chi phí mua sắm một kilôgam thịt trườn là 250 ngàn đồng và số tiền mua một kilôgam thịt heo là 160 ngàn đồng nên số chi phí để sở hữ x kilogam thịt trườn và hắn kilogam thịt heo là: F(x; y) = 250x + 160y (nghìn đồng).
c) Người tớ đang được minh chứng được nhằm số chi phí mua sắm tối thiểu thì (x; y) là tọa chừng của 1 trong những tư đỉnh tứ giác ABCD.
Ta có: F(x; y) = 250x + 160y. Khi đó:
F(0,3; 1,1) = 250 . 0,3 + 160 . 1,1 = 251;
F(0,6; 0,7) = 250 . 0,6 + 160 . 0,7 = 262;
F(1,6; 0,2) = 250 . 1,6 + 160 . 0,2 = 432;
F(1,6; 1,1) = 250 . 1,6 + 160 . 1,1 = 576;
Suy rời khỏi độ quý hiếm nhỏ nhất cần thiết thăm dò là F(0,3; 1,1) = 251.
Vậy nhằm ngân sách là tối thiểu thì mái ấm gia đình cần thiết mua sắm 0,3 kilôgam thịt trườn và 1,1 kilôgam thịt lợn.
Câu 2:
Có nhị hạ tầng khoan giếng A và B. Trung tâm A giá chỉ mét khoan thứ nhất là 8000 (đồng) và Tính từ lúc mét khoan loại nhị, giá chỉ của từng mét sau gia tăng 500 (đồng) đối với giá chỉ của mét khoan ngay lập tức trước cơ. Trung tâm B: Giá của mét khoan thứ nhất là 6000 (đồng) và Tính từ lúc mét khoan loại nhị, giá chỉ của từng mét khoan sau gia tăng 7% giá chỉ của mét khoan ngay lập tức trước cơ. Một doanh nghiệp như là cây xanh ham muốn mướn khoan nhị giếng với chừng sâu sắc theo lần lượt là đôi mươi m và 25 m nhằm đáp ứng phát triển. Giả thiết quality và thời hạn khoan giếng của nhị hạ tầng là như nhau. Công ty ấy nên lựa chọn hạ tầng nào là nhằm tiết kiệm ngân sách ngân sách nhất?
A. Luôn lựa chọn A.
B. Luôn lựa chọn B.
C. Giếng 20m lựa chọn A còn giếng 25m lựa chọn B.
D. Giếng đôi mươi m lựa chọn B còn giếng 25 m lựa chọn A.
Câu 6:
Cho hình chóp S.ABCD có lòng ABCD là hình bình hành. Mặt mặt mũi SAB là tam giác đều cạnh \[\sqrt 3 a\],ABC là tam giác vuông bên trên A có cạnh AC = a, góc thân mật AD và (SAB) bằng 30°. Thể tích khối chóp S.ABCD bằng:
A. \({a^3}\)
B. \(\frac{{\sqrt 3 {a^3}}}{6}\)
C. \(\frac{{\sqrt 3 {a^3}}}{2}\)
D. \(\frac{{\sqrt 3 {a^3}}}{4}\)
