Chủ đề một hình hộp chữ nhật có đáy là hình vuông: Khám huỷ những bí mật của một hình hộp chữ nhật có đáy là hình vuông qua chuyện những biện pháp toán học tập cụ thể và những phần mềm thực tiễn. Từ việc đo lường diện tích S, chu vi, cho tới xác lập thể tích, nội dung bài viết này hỗ trợ tầm nhìn trọn vẹn, giúp cho bạn nắm rõ rộng lớn về cấu tạo và tính phần mềm của hình vỏ hộp vô cuộc sống và công nghiệp.
Hình Hộp Chữ Nhật Có Đáy Là Hình Vuông
Khi xét một hình hộp chữ nhật có đáy là hình vuông, một trong mỗi điều cần thiết cần thiết cảnh báo là đo lường những thông số kỹ thuật tương quan như diện tích S, chu vi và thể tích của hình vỏ hộp này. Bài viết lách sau đây tiếp tục phân tách cụ thể những đo lường cho 1 hình vỏ hộp chữ nhật sở hữu diện tích S lòng là 81 cm2.
1. Định nghĩa và hạ tầng tính toán
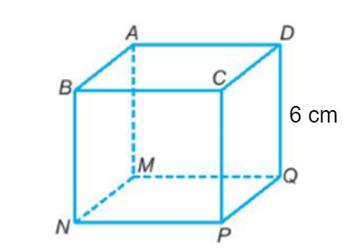
Hình vỏ hộp chữ nhật sở hữu lòng là hình vuông vắn là 1 dạng đặc trưng của hình vỏ hộp chữ nhật, vô tê liệt mặt mũi lòng là 1 hình vuông vắn. Như vậy tức là cả chiều lâu năm và chiều rộng lớn của lòng đều cân nhau.
2. Tính cạnh lòng và chu vi mặt mũi đáy
- Cạnh lòng (a): Vì diện tích S lòng là hình vuông vắn sở hữu diện tích S là 81 cm2, tớ sở hữu \( a = \sqrt{81} = 9 \) centimet.
- Chu vi đáy: Chu vi của lòng là \( Phường = 4 \times a = 4 \times 9 = 36 \) centimet.
3. Tính diện tích S xung xung quanh và toàn phần
- Diện tích xung quanh: Được tính vày công thức \( A_{xung quanh} = Phường \times h \), với \( h \) là độ cao của hình vỏ hộp chữ nhật.
- Diện tích toàn phần: Diện tích toàn phần là tổng diện tích S xung xung quanh và diện tích S nhị mặt mũi lòng, \( A_{toàn phần} = A_{xung quanh} + 2 \times S_{đáy} \).
4. Ví dụ minh họa
Giả sử độ cao của hình vỏ hộp chữ nhật là 10 centimet. Khi đó:
- Diện tích xung quanh: \( A_{xung quanh} = 36 \times 10 = 360 \) cm2.
- Diện tích toàn phần: \( A_{toàn phần} = 360 + 2 \times 81 = 522 \) cm2.
Bài viết lách đang được phân tách cụ thể phương pháp tính những thông số kỹ thuật quan trọng cho 1 hình hộp chữ nhật có đáy là hình vuông. Hy vọng vấn đề này hữu ích cho chính mình gọi trong công việc hiểu và phần mềm vô những vấn đề tương quan.
Tổng quan tiền về hình hộp chữ nhật có đáy là hình vuông
Hình vỏ hộp chữ nhật sở hữu lòng là hình vuông vắn là 1 hình dáng học tập đặc trưng với những cạnh lòng cân nhau, tạo nên sự giản dị tuy nhiên vô nằm trong cần thiết trong số phần mềm thực tiễn. Hình vỏ hộp này không những là 1 quy mô hoàn hảo vô giảng dạy dỗ và tiếp thu kiến thức nhưng mà còn tồn tại nhiều phần mềm vô cuộc sống thường ngày, kể từ phong cách xây dựng cho tới kiến thiết công nghiệp.
- Định nghĩa: Hình vỏ hộp chữ nhật sở hữu lòng là hình vuông vắn là 1 hình vỏ hộp chữ nhật nhưng mà chiều lâu năm và chiều rộng lớn của mặt mũi lòng là cân nhau.
- Tính chất: Các cạnh lòng cân nhau và những góc bên trên mặt mũi lòng là 90 phỏng.
Các thông số kỹ thuật cơ bản:
| Chiều lâu năm cạnh lòng (a) | Được tính kể từ công thức \(a = \sqrt{S_{đáy}}\) nếu như biết diện tích S lòng \(S_{đáy}\). |
| Chu vi lòng (P) | \(P = 4a\) |
| Diện tích xung quanh | \(A_{xung quanh} = Phường \times h\), với \(h\) là độ cao. |
| Diện tích toàn phần | \(A_{toàn phần} = A_{xung quanh} + 2 \times S_{đáy}\) |
| Thể tích | \(V = a^2 \times h\) |
Các quy tắc tính này rất rất hữu ích cho tới việc xử lý nhiều yếu tố vô toán học tập phần mềm tương tự vô kiến thiết nghệ thuật, đáp ứng tính đúng chuẩn và thẩm mỹ và làm đẹp cho những thành phầm sau cùng.
Các công thức đo lường cơ bản
Để hiểu và vận dụng hiệu suất cao hình hộp chữ nhật có đáy là hình vuông trong số vấn đề và phần mềm thực tiễn, việc nắm rõ những công thức đo lường là rất rất cần thiết. Sau đó là những công thức cơ phiên bản cho tới hình vỏ hộp chữ nhật này:
- Diện tích lòng (Sđáy): Tính vày công thức \(S_{đáy} = a^2\), với \(a\) là phỏng lâu năm cạnh của lòng hình vuông vắn.
- Chu vi lòng (P): Tính vày công thức \(P = 4 \times a\).
- Diện tích xung xung quanh (Axung quanh): Tính vày công thức \(A_{xung quanh} = Phường \times h\), với \(h\) là độ cao của hình vỏ hộp.
- Diện tích toàn phần (Atoàn phần): Tính vày công thức \(A_{toàn phần} = A_{xung quanh} + 2 \times S_{đáy}\).
- Thể tích (V): Tính vày công thức \(V = a^2 \times h\).
| Công thức | Biểu thức | Mô tả |
| Diện tích đáy | \(S_{đáy} = a^2\) | Tính diện tích S của mặt mũi lòng hình vuông vắn. |
| Chu vi đáy | \(P = 4a\) | Tính chu vi của mặt mũi lòng hình vuông vắn. |
| Diện tích xung quanh | \(A_{xung quanh} = Phường \times h\) | Diện tích của những mặt mũi xung xung quanh hình vỏ hộp, ko bao hàm mặt mũi lòng và mặt mũi đỉnh. |
| Diện tích toàn phần | \(A_{toàn phần} = A_{xung quanh} + 2 \times S_{đáy}\) | Diện tích toàn cỗ mặt phẳng của hình vỏ hộp, bao hàm cả mặt mũi lòng và mặt mũi đỉnh. |
| Thể tích | \(V = a^2 \times h\) | Thể tích không khí nhưng mà hình vỏ hộp lắc lưu giữ. |
Các công thức này hỗ trợ những kiến thức và kỹ năng toán học tập cơ phiên bản nhằm xử lý nhiều vấn đề tương quan cho tới hình hộp chữ nhật có đáy là hình vuông trong số nghành nghề dịch vụ như phong cách xây dựng, kiến thiết và tạo ra.
Ứng dụng vô thực tiễn của hình hộp chữ nhật có đáy là hình vuông
Hình vỏ hộp chữ nhật sở hữu lòng là hình vuông vắn là 1 hình học tập không những người sử dụng vô toán học tập nhưng mà còn tồn tại nhiều phần mềm thực tiễn vô cuộc sống và công nghiệp. Dưới đó là một vài phần mềm tiêu biểu vượt trội của hình hộp chữ nhật có đáy là hình vuông:
- Kiến trúc và Xây dựng: Hình vỏ hộp này được dùng vô kiến thiết những tòa mái ấm, mái ấm nhằm xe pháo, kho mặt hàng, với cấu tạo giản dị tuy nhiên tối ưu hóa không khí dùng.
- Đóng gói và Lưu trữ: Trong ngành công nghiệp gói gọn, hình hộp chữ nhật có đáy là hình vuông hùn tối ưu hóa không khí tàng trữ và vận gửi sản phẩm & hàng hóa, nhất là những thành phầm rất cần được bảo vệ cảnh giác.
- Thiết nối tiếp nội thất: Các đồ gia dụng thiết kế bên trong như tủ, kệ sách, và những ngăn kéo thông thường được kiến thiết theo mô hình hình hộp chữ nhật có đáy là hình vuông nhằm tăng hiệu suất cao dùng không khí và đơn giản và dễ dàng trong công việc bố trí.
- Giáo dục và Đào tạo: Hình vỏ hộp chữ nhật sở hữu lòng là hình vuông vắn cũng thông thường được dùng trong số bài xích giảng về hình học tập, hùn học viên đơn giản và dễ dàng tưởng tượng và thâu tóm những định nghĩa không khí cơ phiên bản.
- Công nghiệp sản xuất: Trong công nghiệp, những thành phần công cụ thông thường được kiến thiết hình dáng vỏ hộp chữ nhật nhằm đơn giản và dễ dàng vô thi công ráp và duy trì.
Các phần mềm này đã cho thấy vai trò của việc nắm vững về hình hộp chữ nhật có đáy là hình vuông trong số ngành nghề ngỗng không giống nhau, kể từ nghệ thuật cho tới kiến thiết thẩm mỹ và làm đẹp.
Giải những vấn đề tương quan cho tới hình hộp chữ nhật có đáy là hình vuông
Hình vỏ hộp chữ nhật sở hữu lòng là hình vuông vắn là 1 đối tượng người tiêu dùng hình học tập thông thường gặp gỡ trong số vấn đề toán học tập, kể từ giản dị cho tới phức tạp. Dưới đó là một vài ví dụ về phong thái giải những vấn đề tương quan cho tới hình vỏ hộp này:
- Tính thể tích: Để tính thể tích của hình hộp chữ nhật có đáy là hình vuông, dùng công thức \( V = a^2 \times h \), vô tê liệt \( a \) là chiều lâu năm cạnh lòng và \( h \) là độ cao của vỏ hộp.
- Diện tích xung quanh: Diện tích xung xung quanh của hình vỏ hộp rất có thể tính vày công thức \( A_{xung quanh} = Phường \times h \), với \( Phường = 4 \times a \) là chu vi lòng.
- Diện tích toàn phần: Để lần diện tích S toàn phần của hình vỏ hộp, tớ tính \( A_{toàn phần} = A_{xung quanh} + 2 \times a^2 \), với \( 2 \times a^2 \) là tổng diện tích S nhị mặt mũi lòng.
Dưới đó là một ví dụ cụ thể:
- Giả sử một hình hộp chữ nhật có đáy là hình vuông với cạnh lòng 5 centimet và độ cao 10 cm:
- Thể tích của vỏ hộp là \( V = 5^2 \times 10 = 250 \, \text{cm}^3 \).
- Diện tích xung xung quanh là \( A_{xung quanh} = 4 \times 5 \times 10 = 200 \, \text{cm}^2 \).
- Diện tích toàn phần là \( A_{toàn phần} = 200 + 2 \times 25 = 250 \, \text{cm}^2 \).
Các vấn đề về hình hộp chữ nhật có đáy là hình vuông thông thường xuất hiện tại trong số đề thi đua, kể từ giản dị như tính diện tích S, chu vi, cho tới phức tạp hơn hẳn như xác lập tỷ trọng những độ dài rộng lúc biết một vài thông số kỹ thuật chắc chắn.
Câu căn vặn thông thường gặp
Dưới đó là một vài thắc mắc thông thường gặp gỡ về hình hộp chữ nhật có đáy là hình vuông, tất nhiên những phân tích và lý giải và công thức đo lường sẽ giúp các bạn nắm rõ rộng lớn về tính chất toán và phần mềm của mô hình này:
- Câu căn vặn 1: Làm thế nào là nhằm tính diện tích S xung xung quanh của hình hộp chữ nhật có đáy là hình vuông?
- Trả lời: Diện tích xung xung quanh của hình hộp chữ nhật có đáy là hình vuông được xem vày công thức \(A_{xung quanh} = Phường \times h\), với \(P = 4 \times a\) là chu vi lòng và \(h\) là độ cao của vỏ hộp.
- Câu căn vặn 2: Thể tích của hình vỏ hộp chữ nhật này được xem như vậy nào?
- Trả lời: Thể tích được xem vày công thức \(V = a^2 \times h\), vô tê liệt \(a\) là phỏng lâu năm cạnh lòng hình vuông vắn và \(h\) là độ cao của hình vỏ hộp.
- Câu căn vặn 3: Diện tích toàn phần của hình vỏ hộp này là gì?
- Trả lời: Diện tích toàn phần của hình vỏ hộp được xem vày \(A_{toàn phần} = A_{xung quanh} + 2 \times a^2\), với \(a^2\) là diện tích S một phía lòng.
- Câu căn vặn 4: Cách xác lập độ cao của hình vỏ hộp lúc biết thể tích và diện tích S lòng là bao nhiêu?
- Trả lời: Chiều cao \(h\) rất có thể được xác lập vày \(h = \frac{V}{a^2}\), vô tê liệt \(V\) là thể tích đang được biết và \(a^2\) là diện tích S lòng.
Các thắc mắc và vấn đáp này hỗ trợ kiến thức và kỹ năng cơ phiên bản và hữu ích cho tới việc tiếp thu kiến thức và phần mềm toán học tập vô thực tiễn tương quan cho tới hình hộp chữ nhật có đáy là hình vuông.