Cùng lần hiểu những vấn đề cụ thể nhất về tâm đàng tròn trặn nước ngoài tiếp tam giác như khái niệm và những đặc điểm nhập nội dung bài viết bên dưới đây!
Tâm đàng tròn trặn nước ngoài tiếp tam giác là kiến thức và kỹ năng trọng tâm mang đến môn toán hình. Cùng theo dõi dõi nội dung bài viết sau đây nhằm hoàn toàn có thể gia tăng thêm thắt kiến thức và kỹ năng và thích nghi với những dạng bài xích tập luyện không giống nhau nhé.
1. Tâm đàng tròn trặn nước ngoài tiếp nhập tam giác là gì?
Để hoàn toàn có thể nắm rõ và biết phương pháp xác định tâm đàng tròn trặn nước ngoài tiếp tam giác, thứ nhất tất cả chúng ta tiếp tục đi kiếm hiểu định nghĩa và đặc điểm của chính nó tức thì tại đây.
1.1 Khái niệm
Đường tròn trặn nước ngoài tiếp tam giác là đàng tròn trặn trải qua tía đỉnh của một tam giác ngẫu nhiên. Giao điểm của tía đàng trung trực nhập tam giác sẽ tạo nên thành tâm đàng tròn trặn nước ngoài tiếp tam giác bại. Hay nó còn thông thường được gọi là tam giác nội tiếp của hình tròn trụ.
Chẳng hạn, tớ đem ví dụ sau:

Hình hình ảnh minh hoạ về tâm đàng tròn trặn nước ngoài tiếp tam giác ABC
Đường trung trực của AB là đường thẳng liền mạch trải qua trung điểm F của đoạn trực tiếp AB và vuông góc với đoạn trực tiếp AB. Mọi điểm I nhưng mà nằm trong trung trực của đoạn trực tiếp AB đều đều nhau IA = IB.
Có thể thấy rằng, tía đàng trung trực tam giác ABC thì đồng quy bên trên một điểm. Gọi I là vấn đề phú của tía đàng trung trực nhập nhốt giác ABC thì tớ sẽ có được đoạn trực tiếp IA = đoạn trực tiếp IB = đoạn trực tiếp IC. Vì vậy nhưng mà I là tâm đàng tròn trặn nước ngoài tiếp tam giác bại.
1.2 Tính chất
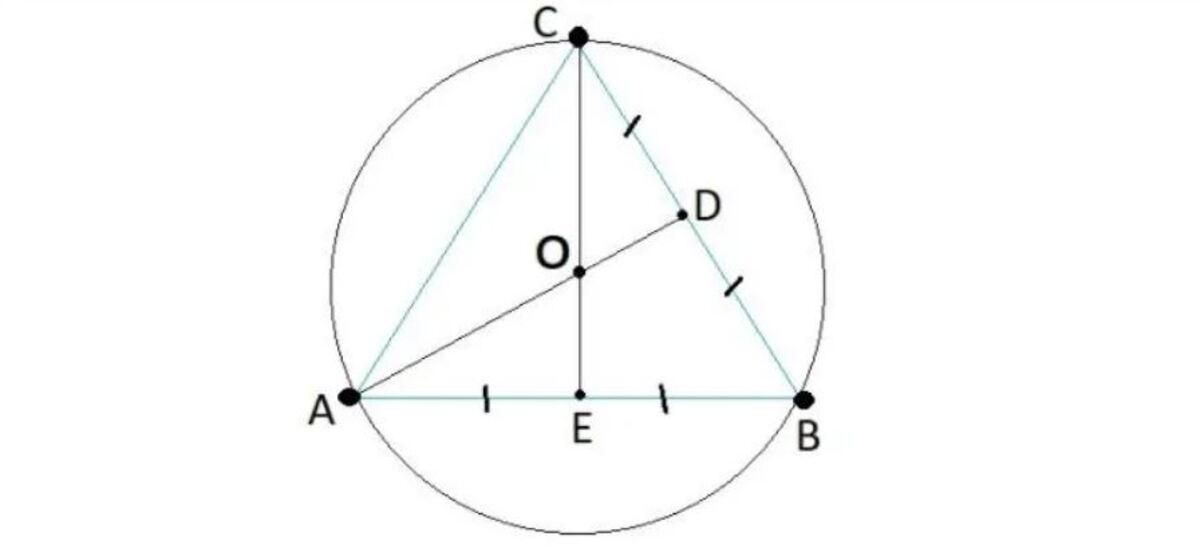 Một số đặc điểm của tâm đàng tròn trặn nước ngoài tiếp tam giác
Một số đặc điểm của tâm đàng tròn trặn nước ngoài tiếp tam giác
Đường tròn trặn nước ngoài tiếp tam giác đem một trong những đặc điểm như sau:
- Mọi tam giác đều chỉ tồn tại một đàng tròn trặn nước ngoài tiếp độc nhất.
- Giao điểm của tía đàng phân giác vuông góc của tam giác vào vai trò là tâm đàng tròn trặn nước ngoài tiếp tam giác và nửa đường kính của chu vi của chính nó được xác lập vì thế khoảng cách thân mật tía đỉnh của chính nó.
- Chính thân mật cạnh huyền vào vai trò là tâm của đàng tròn trặn nước ngoài tiếp tam giác vuông.
- Tâm đàng tròn trặn đem công cộng đàng tròn trặn nước ngoài tiếp tam giác và đàng tròn trặn nội tiếp tam giác đều.
Chẳng hạn: Cho ΔNMP cân nặng bên trên N, nội tiếp đàng tròn trặn (O), đàng cao NH hạn chế (O) ở K. Vì sao NK là 2 lần bán kính của (O)?
Lời giải: Vì tâm O là phú điểm của 3 đàng trung trực của tam giác NMP mà tam giác NMP cân nặng ở N nên đàng cao NH cũng đó là trung trực ⇒ O ∈ NH
Nên: NK là chạc qua loa tâm ⇒ Suy ra: NK là 2 lần bán kính của đàng tròn trặn O
2. Cách xác lập tâm đàng tròn trặn nước ngoài tiếp nhập tam giác
Để hoàn toàn có thể xác lập được tâm đàng tròn trặn nước ngoài tiếp tam giác cần thiết Note một trong những điểm sau:
- Tam giác đem 3 đỉnh cơ hội đều 1 điều thì điểm bại đó là tâm của đàng tròn trặn nước ngoài tiếp tam giác bại.
- Quỹ tích của những điểm coi thanh lịch đoạn trực tiếp AB với cùng 1 góc vuông được xem là đàng tròn trặn đem 2 lần bán kính AB
Ta đem 2 phương pháp để hoàn toàn có thể xác lập được tâm của đàng tròn trặn nước ngoài tiếp tam giác là:
a) Cách 1
Bước 1: Gọi K(x;y) là tâm của đàng tròn trặn nước ngoài tiếp tam giác EFJ. Ta đem những đoạn trực tiếp KE = KF = KJ và vì thế nửa đường kính R
Bước 2: Tọa phỏng tâm K là nghiệm của hệ phương trình:
KE bình phương = KF bình phương
KE bình phương = KJ bình phương
b) Cách 2
Bước 1: Tìm và ghi chép được những phương trình đàng trung trực của nhì cạnh nhập tam giác ngẫu nhiên.
Bước 2: Sau bại, lần phú điểm của hai tuyến phố trung trực vẫn lần rời khỏi ở bước 1 và phú điểm của hai tuyến phố trung trực đó là tâm đàng tròn trặn nước ngoài tiếp tam giác bại.
Tóm lại, tâm của đàng tròn trặn nước ngoài tiếp tam giác NMP cân nặng bên trên N phía trên đàng cao NH và tâm của đàng tròn trặn nước ngoài tiếp tam giác ABC vuông bên trên A là trung điểm cạnh huyền BC.
Cách xác lập tâm đàng tròn trặn nước ngoài tiếp tam giác ABC siêu chi tiết
Để hoàn toàn có thể xác lập được tâm đàng tròn trặn nước ngoài tiếp tam giác Theo phong cách 2, tớ cần thiết tìm kiếm được phương trình của đàng tròn trặn nước ngoài tiếp tam giác lúc biết tọa phỏng 3 đỉnh. Để hoàn toàn có thể giải được câu hỏi về phương trình đàng tròn trặn của nước ngoài tiếp tam giác tớ tiến hành theo dõi quá trình như sau:
Bước 1: Đầu tiên, tớ thay cho tọa phỏng từng đỉnh của tam giác nhập phương trình với ẩn a,b,c (Bởi vì thế những đỉnh của tam giác nằm trong đàng tròn trặn nước ngoài tiếp, nên là, tọa phỏng những đỉnh nhập tam giác vừa lòng phương trình đàng tròn trặn nước ngoài tiếp nhưng mà tớ cần thiết tìm)
Bước 2: Giải hệ phương trình nhằm lần rời khỏi những hằng số a,b,c ứng với những đỉnh nhập tam giác.
Bước 3: Tiếp theo dõi, tớ thay cho độ quý hiếm một vừa hai phải tìm kiếm được như a,b,c nhập phương trình tổng quát lác nhằm lần rời khỏi phương trình đàng tròn trặn nước ngoài tiếp của tam giác.
Bước 4: Do đỉnh của tam giác nằm trong đàng tròn trặn nước ngoài tiếp nên tớ đem hệ phương trình sau:
x(A) bình phương + y(A) bình phương - 2ax(A) - 2by(A) + c = 0
x(B) bình phương + y(B) bình phương - 2ax(B) - 2by(B) + c = 0
x(C) bình phương + y(C) bình phương - 2ax(C) - 2by(C) + c = 0
=> Giải hệ phương trình bên trên tớ tiếp tục tìm kiếm được những hằng số a, b, c.
3. Một số bài xích tập luyện tâm của đàng tròn trặn nước ngoài tiếp tam giác
Để hoàn toàn có thể canh ty chúng ta nắm vững và hiểu rộng lớn những kiến thức và kỹ năng về tâm đàng tròn trặn nước ngoài tiếp tam giác, sau đấy là một trong những bài xích tâp nhằm chúng ta thực hành thực tế.
Bài 1: Cho tam giác ABC vuông bên trên B, và AB = 6cm, BC = 8cm. Q là trung điểm của AC. Hãy xác lập nửa đường kính đàng tròn trặn nước ngoài tiếp tam giác ABC vì thế bao nhiêu?
Giải: gí dụng lăm le lý Pytago, tớ có: CQ = 50% AC
Nên AQ = QB = QC = 5cm
Gọi D là trung điểm AC.
Vì tam giác ABC vuông bên trên B đem BQ là đàng trung tuyến ứng với cạnh huyền AC nên Q là tâm đàng tròn trặn nước ngoài tiếp tam giác ABC.
Suy ra: Đường tròn trặn nước ngoài tiếp tam giác ABC là trung điểm Q của cạnh huyền AC và nửa đường kính đàng tròn trặn nước ngoài tiếp ABC là R = AQ = 5cm
Bài 2: Cho tam giác đều ABC với những cạnh vì thế 12cm. Hãy xác lập tâm và nửa đường kính đàng tròn trặn nước ngoài tiếp tam giác đều ABC? MNP
Giải: Gọi Q, I theo lần lượt là trung điểm của cạnh BC, AB và AQ phú với CI bên trên điểm O.
Vì tam giác đều ABC nên đàng trung tuyến đôi khi cũng chính là đàng cao, đàng phân giác và đàng trung trực của tam giác (tính hóa học tam giác đều)
Vậy nên, O đó là tâm của đàng tròn trặn nước ngoài tiếp tam giác.
Tam giác ABC đem CI là đàng trung tuyến nên CI cũng chính là đàng cao nhập tam giác.
Từ bại, tớ vận dụng lăm le lý Pytago:
CI² = AC² – AI² = 122 – 62 = 108 (cm).
=> CI = 6√3cm.
Vì O là trọng tâm của tam giác ABC nên: CO = 2/3 CI = 2/3 x 6√3 = 4√3 (cm).
Các bài xích tập luyện tự động vận dụng như sau:
Bài 1: Đường cao AD, đàng cao BE của tam giác ABC hạn chế nhau bên trên điểm H (góc C ko cần góc vuông) và hạn chế đàng tròn trặn (O) nước ngoài tiếp tam giác ABC theo lần lượt bên trên N và M.
a, Chứng minh rằng CDHE nội tiếp và xác lập tâm của đàng tròn trặn nước ngoài tiếp của chính nó.
b, Chứng minh tam giác CNM là tam giác cân nặng.
Bài 2: Cho tam giác NMP đem tía góc nhọn nội tiếp nhập đàng tròn trặn (O; R). Ba đàng của tam giác là NF, ME và PD hạn chế nhau bên trên K. Chứng minh tứ giác MDEP là tứ giác nội tiếp. Xác lăm le tâm G của đàng tròn trặn nước ngoài tiếp bại.
Bài 3: Cho tam giác EFJ vuông bên trên E đem EF < EJ, đàng cao EH (H nằm trong EJ). Lấy điểm D sao mang đến H là trung điểm của FD. Gọi A là chân đàng vuông góc hạ kể từ J xuống đường thẳng liền mạch ED. Chứng minh tứ giác EHAJ nội tiếp và xác xác định trí tâm O của đàng tròn trặn nước ngoài tiếp tứ giác bại.
Như vậy, bên trên đấy là tổ hợp loài kiến thức từ không ít bài xích tập luyện, định nghĩa, đặc điểm, loài kiến thức tương quan đến tâm đàng tròn trặn nước ngoài tiếp tam giác. Hy vọng nội dung bài viết này hoàn toàn có thể khiến cho bạn nắm rõ loài kiến thức và lần rời khỏi tiếng giải cho những câu hỏi tương quan.
